We are going to start studying the hertzian dipole:

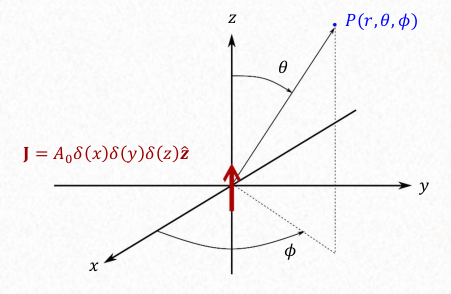
The associated vector A, Magnetic vector potential:

$$ A = \frac{\mu_0 A_0}{ 4 \pi r} e^{-j k_0 r} \hat z \quad [V \cdot s / m] $$ Where:

$$ k_0 = \frac{2 \pi}{\lambda_0} \sqrt{\mu_r \varepsilon_r} $$ Applying the differential operates we can get the fields:

$$ H = \frac{1}{\mu_0} rot \ A \\ E = \frac{1}{j \omega \varepsilon_0} rot \ H $$

The complex poynting vector theorem describe the complex power. The poynting vector is the average of the power density. This is described in 20220929 - Antenna parameters:

$$ S = \frac{1}{2} E \times H^* = \bar S + jQ $$

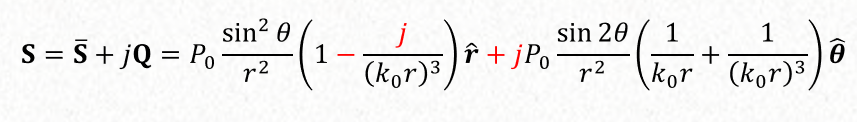
The complex power is the integral of S over a sphere of radious r:

$$ P = \bar P_{rad} + jQ = \frac{1}{2} \int \int_S Re(E \times H^*) \cdot ds = [Watts] $$ Where:

• \(\bar P_{rad}\) is the real time-average power the is radiated to the surrounding space of the antenna.
• \(Q\) is the reactive power and is the imaginary part. It is in the surrounding of the antenna and remains confined to it.

After inserting the field expression into the complex poynting vector we get to the expressions:

$$ \frac{d P_{rad}}{d \Omega} = \frac{1}{2} r^2 \hat r \cdot \bar S = P_0 sin^2 \theta \\ P = \bar P_{rad} + j Q = \eta_0 \big ( \frac{\pi}{3} \big ) \big \lvert \frac{k_0 A_0}{2 \pi} \big \lvert^2 \big ( 1 - \frac{j}{(k_0 r)^3} \big ) $$

From this:

• The reactive power diminishes very fast with the distance, r over 3.

The imaginary part of the complex power is related to the stored energy of the field:

$$ Q = 2 \omega_0 ( \bar W_m - \bar W_e) \qquad \omega_0 = k_0 c_0 $$

$$ Q = - \eta_0 \big ( \frac{\pi}{3} \big ) \big \lvert \frac{k_0 A_0}{2 \pi} \big \lvert^2 \frac{1}{(k_0 r)^3} $$ The value of Q is negative, thus the herztian dipole store more electric energy.

From this we can say that the stored electry energy is larger thatn the stored magnetic energy, thus the hertzian dipole has a capacitive behaviour.

Also the stored energy resides in the radial component of the field.

It is defined the radiation resistance:

$$ R_{rad} = \frac{2 P_{rad}}{I_A^2} \\ R_{rad, hd} = \frac{\eta_0 k_0^2}{6 \pi} \big \lvert \frac{A_0}{I_A} \big \lvert^2 $$ Do not confuse radiation resistance and the antenna’s input impedance. The radiation resistance represents the antenna’s input impedance only if the antenna is lossless and matched to the feeding circuit.

The normalized radiation intensity of a Hertzian dipole is:

$$ F_{HD} = \frac{\bar S}{S_{max}} = sin^2 \theta \\ F_{monopole} = 1 $$ That is the radiation intensity is radiated over \(\theta\), which is the axis of the dipole.

The average radiation intensity will be integratin over the entire sphere and dividing it by the solid angle of a sphere:

$$ F_{av} = \frac{\int \int^S F(\theta, \phi) sin \theta d \theta d \phi}{4 \pi} $$

In terms of poynting vector, power density, it can be express as:

$$ D = \frac{S_{max}}{S_{av}} = \frac{4 \pi r^2 S_{max}}{\bar P_{rad}} $$ Or in terms of radiation intensity:

$$ D = \frac{F_{max}}{F_{av}} \\ D_{HD} = \frac{3}{2} = 1.76 \ dB $$

Effective area

The effective area of the receiving antenna is defined as the ratio of intercepted (received) power 𝑃 and the power density S.

$$ A_e = \frac{\bar P_{rec}}{\bar S_i} \qquad [m^2] \\ A_e = \frac{\lambda_0^2 D}{4 \pi} \\ A_{e,HD} = \frac{3 \lambda_0^2}{8 \pi} $$

Field components

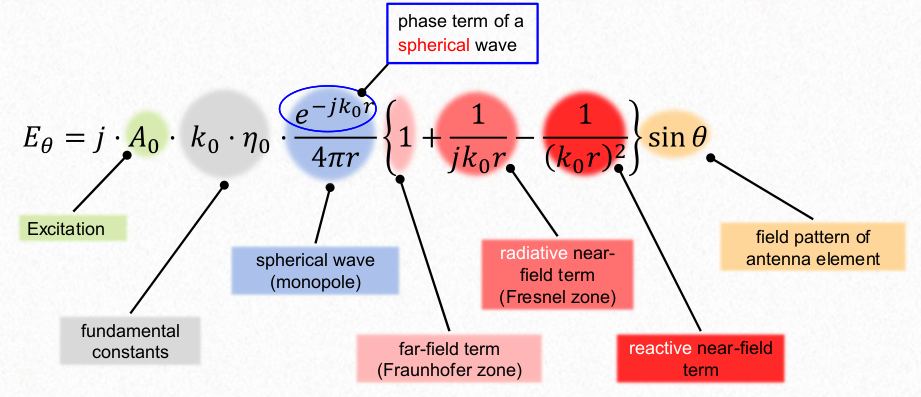
It is definned three regions:

• \(k_0 \ r < 1\): Reactive Near- field region. The complex power is mainly imaginary, decrase inversively to \(r^3\).
• \(1 < k_0 \ r < 2 \ \pi\) Radiative near-field region or Intermediate region: The real part of the power start dominating.
• \(k_0 \ r » 1\) Far-field region. It is the first term that dominates. The complex power is mainly real.

Types of dipoles

Short dipole

$$ l < \lambda_0 / 50 \\ P_0 = \frac{\eta_0}{8} \lvert I_0 \lvert^2 \bigg ( \frac{l}{\lambda_0} \bigg )^2 \\ R_{rad} = \frac{2 \pi}{3} \bigg \lvert \frac{l}{\lambda_0} \bigg \lvert^2 \eta_0 $$

Small dipole

$$ \lambda_0 / 50 < l < \lambda_0 / 10 \\ P_0 = \eta_0 k_0^2 \lvert \frac{I_0 \ l}{8 \pi} \lvert^2 \\ R_{rad} = \frac{\pi}{6} \bigg \lvert \frac{l}{\lambda_0} \bigg \lvert^2 \eta_0 $$

Arbitrary length

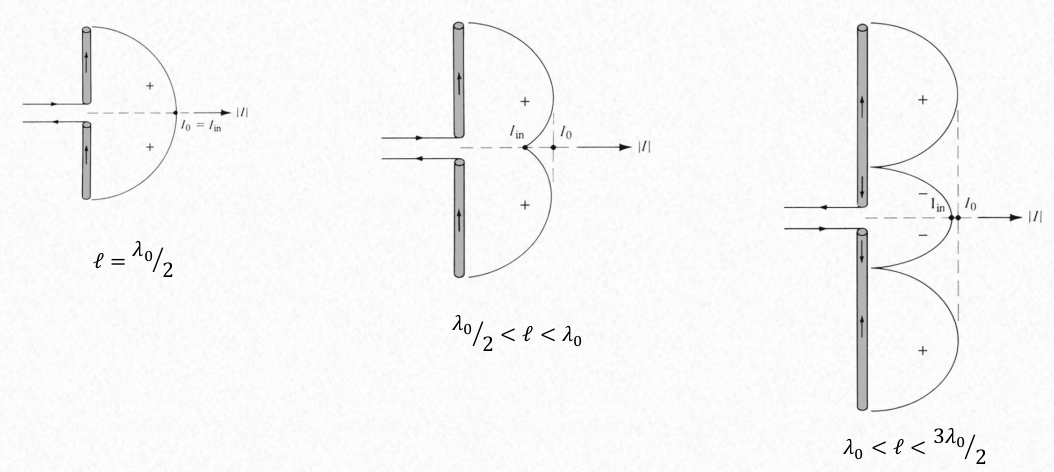
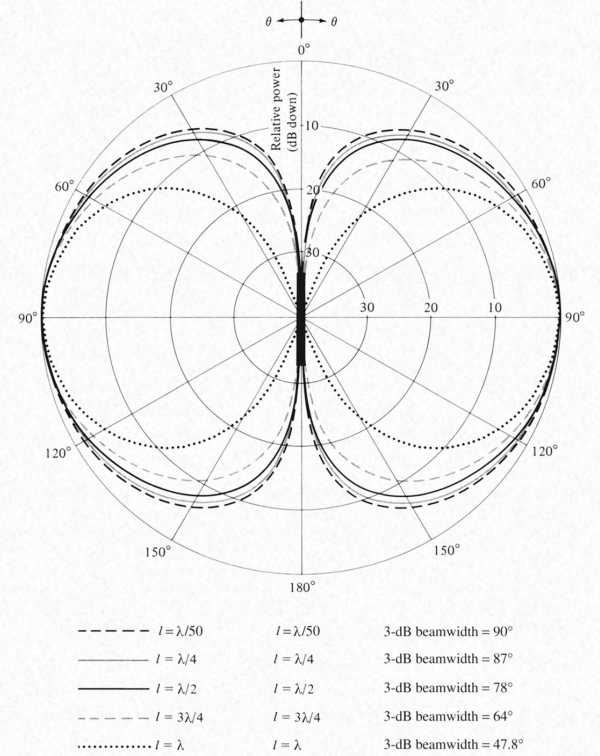
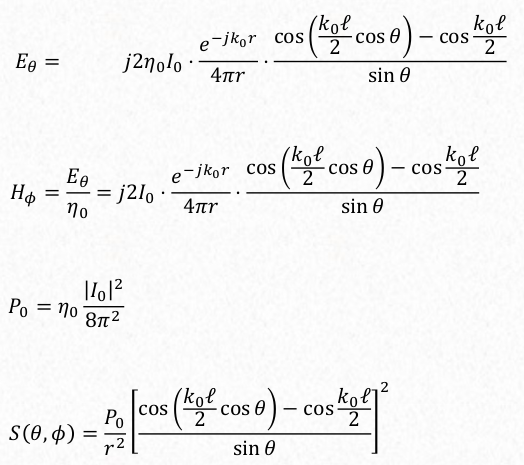
The input resistance of a dipole is infinite if it is bigger. The dipole has input impedance of 50 ohms when it is of length 0.5 lambda.