Amplificador diferencial

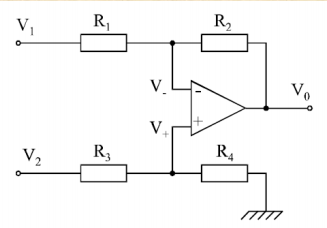
Solución del circuito por Kirtchoff:

$$ V_o = V_2 \frac{R_4}{R_3 + R_4} \ \big ( \frac{R_2}{R_1} + 1 \big ) - V_1 \frac{R_2}{R_1} \\ $$ $$ V_o = \frac{R_2}{R_1} \cdot (\frac{1+R_1/R_2}{1+ R_3/R_4}V_2 - V_1) = A_2 \cdot V_2 + A_1 \cdot V_1 \\ A_2 = (1 + \frac{R_2}{R_1})\cdot \frac{R_4}{R_3+R_4} \qquad A_1 = - \frac{R_2}{R_1} $$

Solución del circuito por superposición:

$$ V_1 = V_c + \frac{V_d}{2} \qquad V_2 = V_c - \frac{V_d}{2} \\ V_{d} = V_2 - V_1 \qquad V_{c} = \frac{V_1 + V_2}{2} \\ G_d = \frac{V_0}{V_d} \lvert_{v_c = 0} \qquad G_c = \frac{V_0}{V_c} \lvert_{v_d = 0} \\ V_o = G_d \cdot V_d + G_c \cdot V_c = A_2 \cdot V_2 + A_1 \cdot V_1 \\ G_d = \frac{1}{2} \cdot (A_2 - A_1) = - \frac{1}{2} \bigg [ \frac{R_4}{R_3 + R_4} (1 + \frac{R_2}{R_1} ) + \frac{R_2}{R_1} \bigg ] \\ G_c = A_2 +A_1 = \frac{R_4 \ R_1 - R_2 \ R_3}{(R_3 + R_4) \ R_1} $$

Hay una forma más elegante que es cómo lo hacemos en 20201110 - Apuntes 1er parcial SEAM.

En cambio en esta asignatura se hace más rápidamente aplicando el teorema de superposición que básicamente se referira a lo siguiente: $$ V_o = V_o(V_1, V_2) = V_o(V_1, 0) + V_o(0, V_2) \\ \text{Se definen} \quad V_{d} = V_2 - V_1 \qquad V_{c} = \frac{V_1 + V_2}{2} \\ V_o = G_d \cdot V_d + G_c \cdot V_c \\ $$ Se define la Relación de Rechazo al Modo Común (CMRR):

$$ CMRR = 20 \ \log{\frac{G_d}{G_c}} $$

Para anular \(G_c\) debe de cumplirse: $$ G_c = 0 \Rightarrow R_4 \ R_1 = R_2 \ R_3 \\ \frac{R_2}{R_1} = \frac{R_4}{R_3} = \alpha \Rightarrow G_d = - \alpha $$

Cálculo de la impedancia de entrada

Para calcular \(Z_{i1}\) ponemos un generador de tensión a la entrada con valor de tensión E y valor de corriente I, y conectamos \(V_2\) a masa. Calculamos el valor de la tensión y concluimos con \(Z_{i1} = \frac{E}{I}\).

Lo mismo para la otra entrada.

Puente de impedancias

Puente Wheatstone

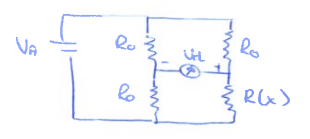
$$ V_d = V_A \bigg [ \frac{R(x)}{R(x) + R_0} - \frac{1}{2} \bigg ] $$

Si me piden quitar el efecto parásito de algún componente. Una solución es este puente con un sensor ciego encima de R(x), siendo este de valor R(0).

Visto de otro ejercicio: Un puente como este, en el que tres de las impedancias son fijas e iguales y solo una varía, presenta la máxima sensibilidad si el valor de las impedancia fijas coincide con el de la que varía en ausencia de estímulo de entrada, en nuestro caso cuando \(\Delta l = 0\). Por tanto, el valor más adecuado para los condensadores fijos \(C_0\) es:

$$ C_0 = C(\Delta l = 0) $$

Semipuente

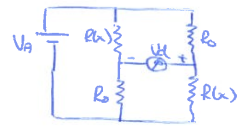
$$ V_d = V_A \bigg [ \frac{R(x)}{R(x) + R_0} - \frac{R_0}{R_0 + R(x)} \bigg ] $$

Puente push-pull

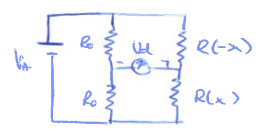
$$ V_d = V_A \bigg [ \frac{R(x)}{R(x) + R(-x)} - \frac{1}{2} \bigg ] $$

Puente completo

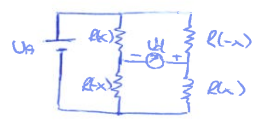
$$ V_d = V_A \bigg [ \frac{R(x)}{R(x) + R(-x)} - \frac{R(-x)}{R(-x)+R(x)} \bigg ] $$

Autocalentamiento

$$ \Delta T = \beta T_d = \beta \ I^2 \ R(x) \\ \Delta T = \beta \ I^2 \ R(\varepsilon = 0, \Delta T) $$

Ejercicio autocalentamiento

1.2.- Considerando que el extensímetro tiene un coeficiente térmico α y que el coeficiente de autocalentamiento es β, calcule el error aparente debido al autocalentamiento.

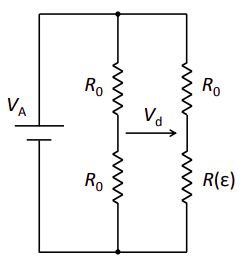
$$ R(\varepsilon) = R_0 \ (1 + S \ \varepsilon) \\ V_d = V_A \cdot \bigg [ \frac{R(\varepsilon)}{R_0 + R(\varepsilon)} - \frac{1}{2} \bigg ] \\ V_d = \frac{V_A}{2} \cdot \frac{S \ \varepsilon}{2 + S \ \varepsilon} $$

El error del enunciado afectará de la siguiente forma: $$ R(\varepsilon, \Delta T) = R_0 \ (1 + S \ \varepsilon)(1 + \alpha \ \Delta T) $$

Se definirá el autocalentamiento de la siguiente forma: $$ \Delta T = \beta \ I^2 \ R(\varepsilon = 0, \Delta T) \\ = \beta \cdot \bigg ( \frac{V_A}{R_0 + R_0(1 + \alpha \ \Delta T)} \bigg )^2 \cdot R_0(1 + \alpha \Delta T) $$

Como en los extensiometros metálicos tienen una dependencia con la temperatura muy pequeña suponemos que \(\alpha \Delta T = 0\) $$ \Delta T = \beta \cdot \bigg ( \frac{V_A}{R_0 + R_0} \bigg )^2 \cdot R_0 \\ = \beta \frac{V_A^2}{4 \ R_0} $$

Para calcula el error aparente hacemos lo hacemos de la siguiente forma: $$ V_d(\varepsilon = 0, \Delta T) = \frac{V_A}{2} \cdot \frac{\alpha \Delta T}{2 + \alpha \ \Delta T} \\ V_d(\varepsilon_{ap}, \Delta T = 0) = \frac{V_A}{2} \cdot \frac{\varepsilon \ S}{2 + \varepsilon \ S} $$

$$ V_d(\varepsilon = 0, \Delta T) = V_d(\varepsilon_{ap}, \Delta T = 0) \\ \Rightarrow \varepsilon_{ap} S = \alpha \ \Delta T \\ \varepsilon_{ap} = \frac{\alpha}{S} \ \Delta T = \frac{\alpha}{S} \ \beta \frac{V_A^2}{4 \ R_0} $$