Bocata hizo un video explicando el primer parcial lo dejo por aquí

Configuración amplificadora no inversora (CANI)

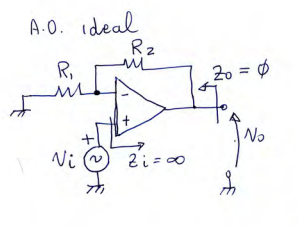
$$ G_V = \frac{V_o}{V_i} = 1 + \frac{R_2}{R_1} $$

En CANI supongo que \(I_N = I_P = I_B\)

Configuración amplificadora inversora (CAI)

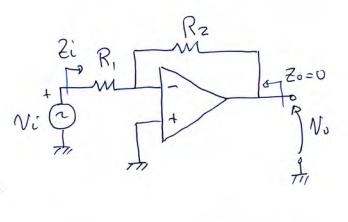$$ G_V = \frac{V_o}{V_i} = - \frac{R_2}{R_1} $$

En CAI supongo que \(I_N = I_P = I_B\)

Primer ejercicio - Cálculo de CMRR

Tal que un amplificador restador tiene la siguiente salida: $$ V_o = \frac{R_2}{R_1} \cdot (\frac{1+R_1/R_2}{1+ R_3/R_4}V_2 - V_1) = A_2 \cdot V_2 + A_1 \cdot V_1 \\ A_2 = (1 + \frac{R_2}{R_1})\cdot \frac{R_4}{R_3+R_4} \qquad A_1 = - \frac{R_2}{R_1} $$

Si el puente está balanceado \(R_1/R_2 = R_3 / R_4\) entonces: $$ V_o = \frac{R_2}{R_2}(V_2 - V_1) $$

Se define entonces: $$ V_{id} = V_2 - V_1 \qquad V_{ic} = \frac{V_1 + V_2}{2} $$

$$ V_1 = V_{ic} - \frac{V_{id}}{2} \qquad V_2 = V_{ic} + \frac{V_{id}}{2} $$

Con lo que se definen las ganancias como: $$ A_{dm} = \frac{V_{od}}{V_{id}} \big \lvert_{V_{ic}=0} \qquad A_{cm} = \frac{V_{oc}}{V_{ic}} \big \lvert_{V_{id}=0} $$

Entonces. Llegamos a lo siguiente: $$ V_o = V_{od} + V_{oc} = A_{dm}\cdot V_{id} + A_{cm} \cdot V_{ic} = A_2 \cdot V_2 + A_1 \cdot V_1 $$

Operando la expresión anterior se llega a lo siguiente: $$ V_o = A_2 \cdot (V_{ic} + \frac{V_{id}}{2}) + A_1 \cdot (V_{ic} - \frac{V_{id}}{2}) = V_{ic}\cdot (A_1+A_2) + 1/2 \cdot V_{id}(A_2 - A_1) $$

Con lo que se llega a la conclusión de que:

$$ A_{dm} = \frac{1}{2} \cdot (A_2 - A_1) \qquad A_{cm}= A_2 +A_1 $$

Y para hayar el CMRR se opera de la siguiente manera: $$ CMRR_{dm} = 20 \cdot \log \lvert \frac{A_{dm}}{A_{cm}} \lvert $$

Segundo ejercicio - Tensión de offset

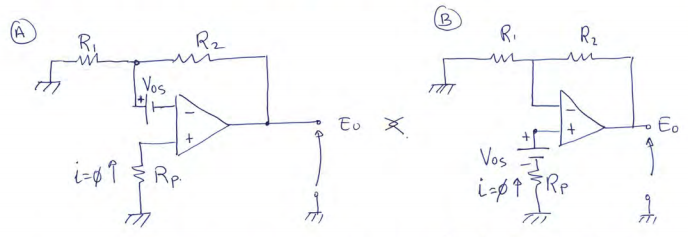
Los dos circuitos son análogos. $$ \frac{0-V_{os}}{R_1} = \frac{V_{os}-E_0}{R_2} \Rightarrow E_o = (1 + \frac{R_2}{R_2})\cdot V_{os} $$

Segundo ejercicio - Corrientes de polarización

Existen las corrientes de polarización \(I_P\) y \(I_N\). Se definen: $$ \text{Input Biass Current} = I_B = \frac{I_P + I_N}{2} \\ \text{Input Biass Current Offset} = I_{OS} = I_P - I_N $$

Lo que implica: $$ I_P = I_B + 1/2 \cdot I_{OS} \qquad I_N = I_B - 1/2 \cdot I_{OS} $$

Se trabaja con Ip e In de manera independiente, y se calcula su efecto en la salida por superposición de ambas.

Tensión de error en la salida producida por las corrientes de polarización: $$ E_{OIP} = E_O \lvert_{I_N = 0} \\ E_{OIN} = E_O \lvert_{I_P = 0} \\ E_{OIB} = E_{EOIP} + E_{OIN} $$

Segundo ejercicio - Slew-Rate (SR)

SR = Máxima velocidad de variación de la tensión. Parámetro no lineal de gran señal. Cuando aparece, el AO deja de cumplir que \(V_P = V_N\)

Se define la amplitud máxima del escalon para que no aparezca distorsión por SR: $$ V_{om} = \frac{SR}{2 \cdot \pi f_H} = \frac{SR}{2 \cdot \pi \beta \cdot f_t} $$

El desarrollo biene de: $$ SR = \frac{d \ V_0}{d \ t} \lvert_{max} \\ V_o(\omega t) = V_0 \sin{(\omega \ t)} + E_{ODC} \\ \frac{d \ V_0}{d \ t} = V_0 \omega \cos{\omega \ t} \Rightarrow SR = \frac{d \ V_0}{d \ t} \lvert_{max} = 2 \ \pi \ f \ V_o \\ V_{om} = \frac{SR}{2 \cdot \pi f_H} = \frac{SR}{2 \cdot \pi \beta \cdot f_t} $$

Tercer ejercicio - Schmitt trigger inversor

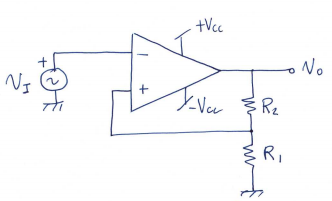
Vo puede ser Voh o Vol: $$ V_{TH} = \frac{R_1}{R_1 + R_2} \cdot V_{OH} \\ V_{TL} = \frac{R_1}{R_1 + R_2} \cdot V_{OL} $$

Tercer ejercicio - Smitt trigger no inversor

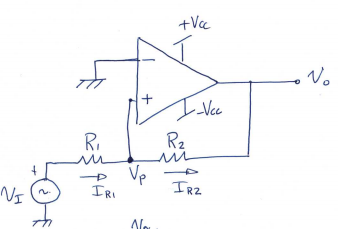
Vo puede ser Voh o Vol: $$ V_{TH} = -\frac{R_1}{R_2} \cdot V_{OL} \\ V_{TL} = -\frac{R_1}{R_2} \cdot V_{OH} $$

Tercer ejercicio - Montaje 555

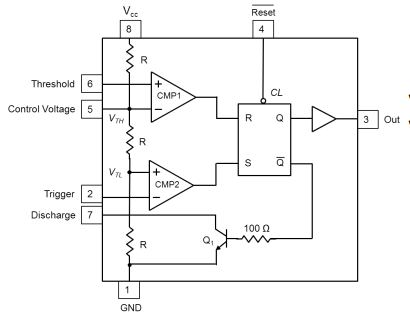
En el montaje 555: $$ V_{TH} = \frac{2}{3} \cdot V_{CC} \\ V_{TL} = \frac{1}{3} \cdot V_{CC} $$

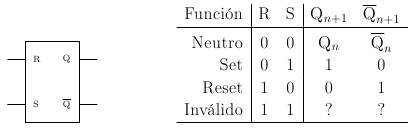
Monoestable

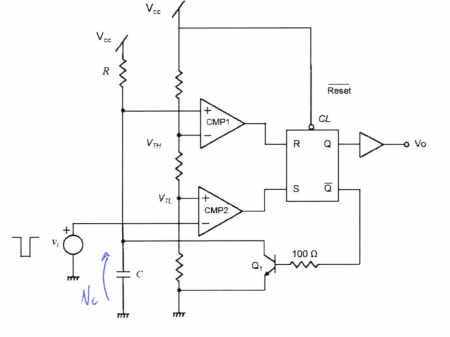
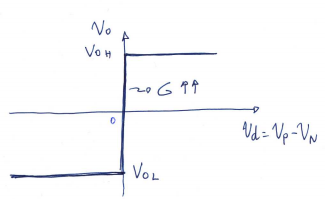
$$ V_o = V_{oH} \quad \text{si} \quad V_p > V_n \\ V_o = V_{oL} \quad \text{si} \quad V_p < V_n $$

Cuando \(\overline{Q} \) es 1 \(Q_1\) está conduciendo, lo que hace que C esté a masa (descargandose). Cuando \(\overline{Q}\) es 0 \(Q_1\) está cortado, lo que hace que se carge C con RC.

Tiempo de T es: $$ T = RC \ \ln{[\frac{V_{\inf} - V_0}{V_{\inf} - V_1}]} $$