Bocata hizo un video explicando el primer parcial. Y lo dejo por aquí
Primer ejercicio de filtros
El primero consistirá en mirar una tabla, elegir un orden y hacer el filtro.
Transformación de frecuencias
$$ \text{Paso bajo} \quad \Rightarrow f_{0} = f_c \cdot f_{0_{LP(tabla)}} \\ \text{Paso alto} \quad \Rightarrow f_{0} = \frac{f_c}{f_{0_{LP(tabla)}}} $$
Filtro de primer orden
Paso Bajo
$$ H(j\omega) = \frac{1}{1 + j\omega/\omega_0} \\ \omega_0 = \frac{1}{RC} $$
Paso Bajo con ganancia
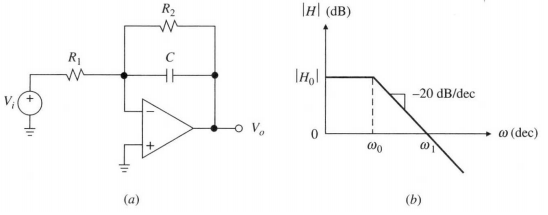
$$ H(j \omega) = H_0 \frac{1}{1 + j \omega/ \omega_0} \\ H_0 = -\frac{R_2}{R_1} \\ \omega_0 = \frac{1}{R_2 C} $$
Polo en \(s = - \omega_0\)
Paso Alto
$$ \omega_0 = \frac{1}{RC} \\ H(j\omega) = \frac{j\omega/\omega_0}{1 + j \omega / \omega_0} $$
Paso Alto con ganancia
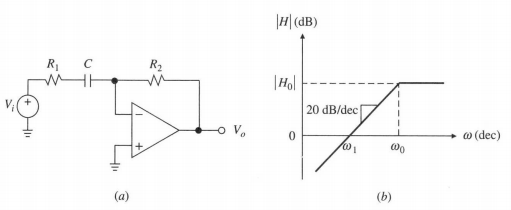
$$ H(j \omega) = H_0 \frac{j \omega / \omega_0}{1 + j \omega/ \omega_0} \\ H_0 = -\frac{R_2}{R_1} \\ \omega_0 = \frac{1}{R_1 C} $$
Cero en \(s = 0\) y Polo en \(s = - \omega_0\)
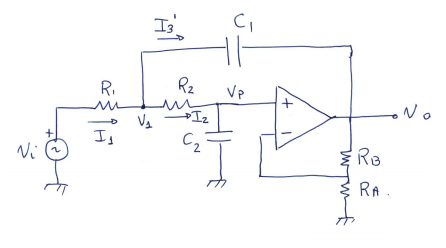
Filtro de segundo orden
El filtro Sallen-Key será de la siguiente forma:
Paso Bajo
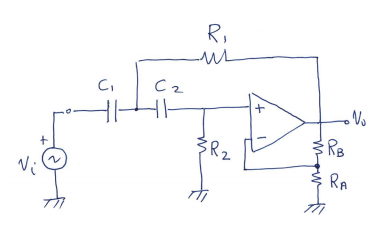
Paso Alto
Filtro KRC con componentes iguales
- Fácil de ajustar
- Sensible a Q: Si Q es alta, K se aproxima a 3 V/V pero debe mantenerse K<3
- Si \(K \ge 3 \Rightarrow\) Q negativo, polos en RHP, la realimentación positiva supera a la realimentación negativa => riesgo de oscilación a \(\omega_0\)!!
$$ R_1 = R_2 = R \qquad C_1 = C_2 = C \\ H_{0LP} = k \qquad k = 3 - \frac{1}{Q} \\ \omega_0 = \frac{1}{R \ C} \qquad R_B = (k - 1)\cdot R_A $$
Filtro KRC con ganancia unidad
- Tiene menos componentes porque \(R_A\) será circuito abierto y \(R_B\) será circuito cerrado.
- Menos componentes, mayor BW: \(f_H \approx f_t\)
- \(\omega_0\) y Q son interdependientes
- Resulta adecuado para Q alta
$$ R_2 = R \qquad R_1 = m \cdot R \\ C_2 = C \qquad C_1 = n \cdot C \\ \omega_0 = \frac{1}{\sqrt{m \cdot n} \cdot RC} \\ \text{Paso Bajo} \quad Q = \frac{\sqrt{m \cdot n}}{m + 1} \qquad n \ge 4 \cdot Q^2 \\ \text{Paso Alto} \quad Q = \frac{\sqrt{n / m}}{n + 1} \qquad n = 1 \Rightarrow C_1 = C_2 $$
Para la configuración de paso bajo:
$$ Q_{max} \quad \text{con} \quad m = 1 \\ \text{Si elegimos} \quad m = 1 \Rightarrow n = 4Q^2 \Rightarrow C_1 > C_2 \quad \text{Problema si Q alto} $$
Opción práctica de diseño para paso bajo:
$$ \text{elegir} \quad n \ge 4Q^2 \Rightarrow C_1, C_2 \\ m = A + \sqrt{A^2 - 1} \qquad A = \frac{n}{2 Q^2} - 1 $$
Corregir la ganancia de una etapa
Ha veces nos piden modificar la ganancia del filtro. Para ello se pondrán una resistencias en forma que dividan la tensión. Se calculará de la siguiente forma (extraido de la 20201106 - Practica 1 SEAM - Francisco Jesús Acién Pérez):
El filtro tendrá una ganancia de \(k = 2.29\) con lo que habrá que corregirla de la siguiente forma:
$$ A_{new} = \frac{R_{1B}}{R_{1A}+R_{1B}} \qquad R_1 = R_{1A}//R_{1B} \\ R_{1A} = R_1 \frac{A_{old}}{A_{new}} \qquad R_{1B} = \frac{R_1}{1-A_{new}/A_{old}} $$
Queremos lograr que la ganancia del filtro sea la unidad, con lo que \(A_{new} = 1\). Con lo que obtenemos lo siguiente.
$$ R_{1A} = R_1 \frac{2.29}{1} = 2776.3 \ \Omega \\ R_{1B} = \frac{R_1}{1 - 1/2.29} = 2156.9 \ \Omega $$
Se podrá el filtro de la siguiente forma:
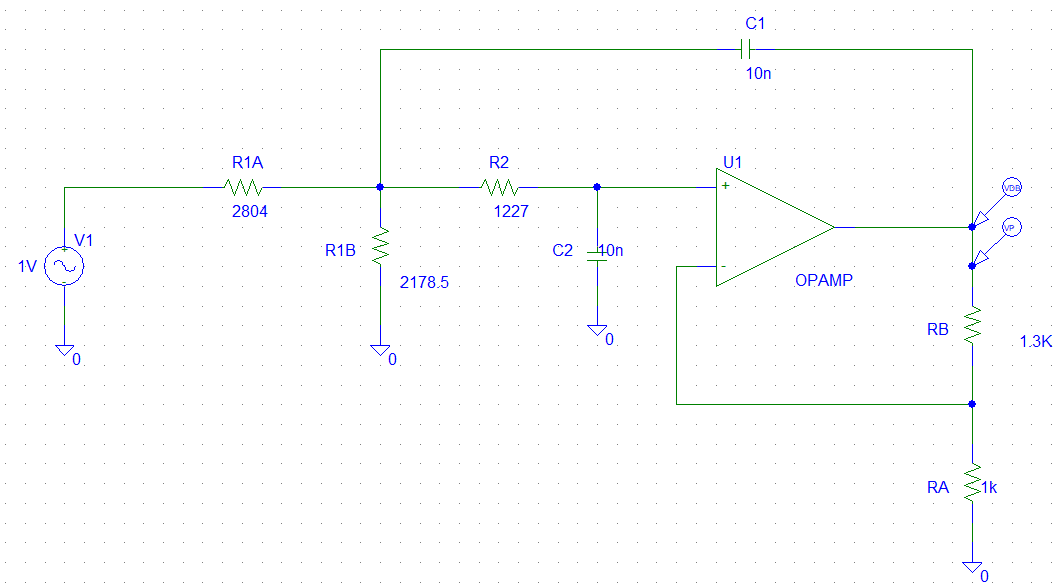
Notese la disposición de \(R_{1A}\) \(R_{1B}\).
Disposición de las etapas
Si las etapas se ordenan de Q creciente se optimiza el margen dinámico de entrada (la ganancia se dispara con Q alto).
Si se ordenan con Q decreciente se mejora el comportamiento con el ruido interno, que se amplifica alrededor de \(\omega_0\) en las etapas con Q alto.
Valores arbitrarios resistencias y condensadores
Para resolver los ejercicos se elige un valor arbitrario para las resistencias y condensadores. Usaré el siguiente que es el más común:
$$ R_A = 10 \ K\Omega \\ C = 1 \ nF $$
Segundo ejercicio Amplificadores
Algunas cosas de amplificadores:
$$ \text{Rendimiento} \qquad \eta = \frac{P_L}{P_{IN}} \\ P_L = \text{Potencia entregada a la carga } \ R_L \\ P_{IN} = \text{Potencia suministrada por las fuentes de alimentación } \ \pm V_{cc} \\ \eta_A = \frac{1}{4}\big(\frac{V_L}{V_{CC}}\big)^2 \\ \eta_B = \frac{P_L}{P_{IN}} = \frac{\pi}{4}\cdot \frac{V_L}{V_{CC}} $$
Se definirá en la mayoría de los casos: $$ P_{IN_{max}} = 2 \cdot V_{CC} \cdot <I_{CC_{max}}> = 2 \cdot V_{CC} \cdot \frac{I_{CC_{max}}}{\pi} $$ Donde se multiplica por 2 porque estamos contado la potencia suministrada en el ciclo positivo y en el ciclo negativo.
Se define: $$ P_D = \text{Potencia disipada por el amp} \\ P_D = P_{IN} - P_L = \frac{P_L}{\eta} - P_L = (\frac{1}{\eta} - 1) \cdot P_L $$
Algunas cosas más para refrescar conceptos: $$ \text{Potencia instantánea: } \ P_i(t) = V_i(t) \cdot I_i(t) \\ \text{Potencia media: } P_m(t) = \frac{1}{T} \int_{0}^{T} P_i(t) \cdot dt \\ = < P_i(t) > = \overline{P_i(t)} $$
Para una señal sinusoidal la potencia será: $$ \begin{cases} V_L(t) = V_p \cdot \sin{(\omega \ t)} \\ i_L(t) = \frac{V_p}{R_L} \cdot \sin{(\omega \ t)} \end{cases} \\ P_L = <P_{Li(t)}> = \int_{0}^{T} \frac{V_p^2}{R_L} \sin^2 (\omega t) \cdot dt = \frac{1}{2}\frac{V_p^2}{R_L} $$
Para una señal cuadrada será: $$ P_{Lm} = \frac{V_p^2}{R_L} $$
La potencia disipada por un transistor (o otro componente) será: $$ P_{Q1} = \frac{1}{2} \cdot (P_{IN} - P_{Lmax}) $$
Clase A
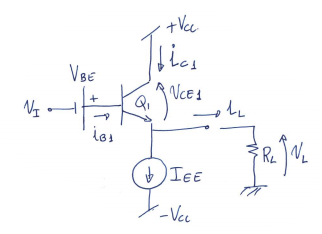
Características ideales:
- \(V_{L_{max}} \approx \pm V_{cc}\)
- Baja distorsión
- \(\eta < 25\%\)
- Sin condesador de desacoplo
- Alimentación simétrica
Reposo
$$ V_L = V_I = 0 \\ i_L = 0 \\ \Rightarrow i_{c1} = \beta i_{B1} = I_{EE} \\ V_{CE1} = V_{CC} $$
Con lo que en reposo consume.
Ciclo positivo
Esto es \(V_I > 0\)
Si \(V_I \uparrow, i_{c1} \uparrow , i_l \ \text{saliente}, V_L > 0 , V_{CE1} \downarrow\)
$$ V_{L_{max}}^+ = V_{cc} - V_{CE_{sat1}} \approx V_{CC} \quad \text{(Q1 en saturación)} \\ i_{L_{max}}^+ = \frac{V_{L_{max}}^+}{R_L} \approx \frac{V_{CC}}{R_L} $$
Ciclo negativo
Esto es \(V_I < 0\)
Si \(V_I \downarrow, i_{c1} \downarrow , i_l \ \text{entrante}, V_L < 0 , V_{CE1} \uparrow, V_{I_{EE} \downarrow}\)
Puede ocurrir la saturación de la fuente \(I_{EE}\)
$$ V_{L_{max}}^- = -V_{cc} + V_{SAT_{I_{EE}}} \approx - V_{CC} \\ i_{L_{max}}^- = \frac{V_{L_{max}}^-}{R_L} \approx - \frac{V_{CC}}{R_L} $$
O puede ocurrir el corte de Q_1
$$ V_{L_{max}}^- = -I_{EE} \cdot R_L \\ i_{L_{max}}^- = - I_{EE} $$
Margen dinámico en la salida
Para hacer el margen dinámico en la salida se prefija el valor:
$$ I_{EE} = \frac{V_{CC}}{R_L} $$
De esta forma se cumplira que: $$ i_{l_{max}}^+ = I_{EE} \\ i_{l_{max}}^- = -I_{EE} $$
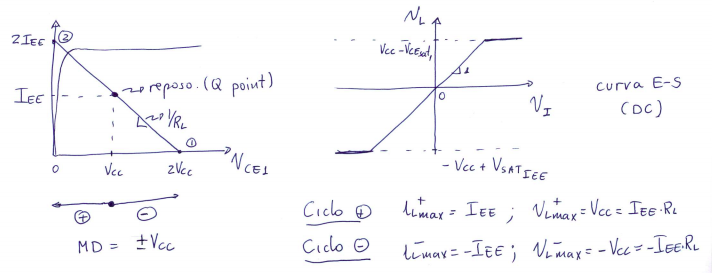
Nota: la gráfica de la derecha es \(i_{c_1}\) sobre \(V_{CE_{1}}\)
Rendimiento amplificador de clase A
$$ \eta_A = \frac{1}{4}\big(\frac{V_L}{V_{CC}}\big)^2 $$
Clase B
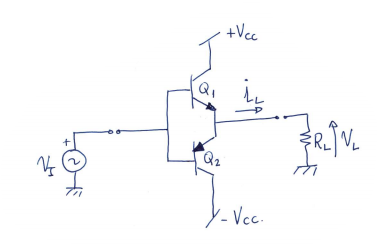
- Por complementario NPN-PNP
- \(Q_1\) y \(Q_2\) apareados
- \(V_{gamma} = V_{BE1} = V_{EB2} \approx 0.7 \ V\)
- \(V_{BE1} + V_{EB2} = 0\)
- \(Q_1\) y \(Q_2\) nunca conducen simultáneamente
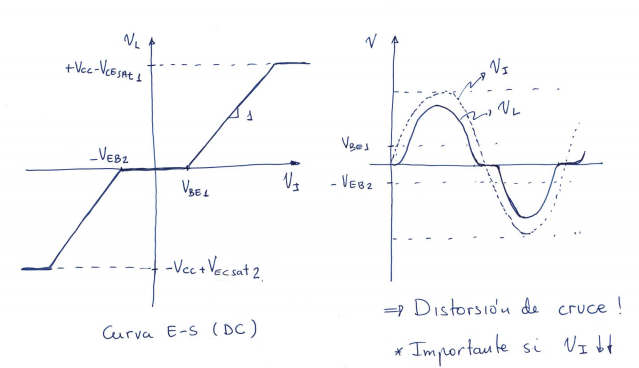
La distorisión de cruce se puede reducir mediante 2 técnicas:
- Amplificador de clase AB
- Realimentación negativa con A.O.
Ciclo de reposo
$$ V_I = 0 \Rightarrow \begin{cases} Q_1 \ \text{cortado} \\ Q_2 \ \text{cortado} \end{cases} \Rightarrow \begin{cases} i_L = 0 \\ V_L = 0 \end{cases} $$
\(Q_{1,2}\) se mantienen cortados si \(-V_{\gamma} < V_I < V_{\gamma} \Rightarrow P_{in} = 0\)
Ciclo positivo
$$ V_I > V_{\gamma} = 0.7 \ V \begin{cases} Q_1 \ \text{activa} \\ Q_2 \ \text{cortado} \end{cases} \Rightarrow \begin{cases} i_L \ \text{saliente} \\ V_L = V_I - V_{BE1} \approx V_I - 0.7 \ V \end{cases} $$
$$ V_{L_{max}}^+ = V_{CC} - V_{CE_{sat1}} \approx V_{CC} \\ i_{L_{max}}^+ = \frac{V_{L_{max}}^+}{R_L} \approx \frac{V_{CC}}{R_L} $$
Ciclo negativo
$$ V_I < -V_{\gamma} = -0.7 \ V \begin{cases} Q_1 \ \text{cortado} \\ Q_2 \ \text{activa} \end{cases} \Rightarrow \begin{cases} i_L \ \text{entrante} \\ V_L = V_I - V_{BE2} \approx V_I + 0.7 \ V \end{cases} $$
$$ V_{L_{max}}^- = -V_{CC} + V_{CE_{sat2}} \approx -V_{CC} \\ i_{L_{max}}^- = \frac{V_{L_{max}}^-}{R_L} \approx -\frac{V_{CC}}{R_L} $$
Rendimiento
El rendimiento de los amplificadores de tipo B y AB será: $$ \eta_B = \frac{P_L}{P_{IN}} = \frac{\pi}{4}\cdot \frac{V_L}{V_{CC}} $$
Clase AB
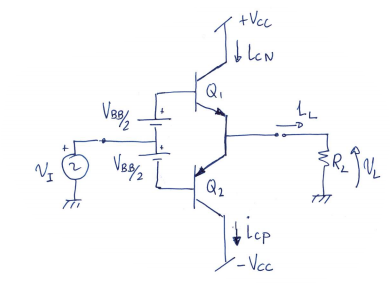
- \(Q_1\), \(Q_2\) polarizados justo encima del corte, en activa con \(I_{C1,2} \downarrow\)
- Suponiendo que \(Q_1\), \(Q_2\) están apareados:
- \(I_{CN} = I_S \cdot e^{V_{BE1}/V_T}\)
- \(I_{CP} = I_S \cdot e^{V_{EB2}/V_T}\)
Se cumple que: $$ V_{BE1} + V_{EB2} = V_{BB} $$
$$ \eta_B = \frac{P_L}{P_{IN}} = \frac{\pi}{4}\cdot \frac{V_L}{V_{CC}} $$
Ciclo de reposo
Ambos transistores conducen con la misma corriente (se diseña para que sea pequeña, para tener un consume en reposo pequeño \(P_{in} \downarrow \downarrow\))
$$ V_I = 0 \Rightarrow V_{BE1} = V_{EB2} = V_{BB}/2 \\ i_{cn} = i_{cp} \Rightarrow \begin{cases} i_L = 0 \\ V_L = 0 \end{cases} \\ P_{in} \neq 0 \qquad Q1, Q2\text{ disipan potencia} $$
Ciclo positivo
$$ V_I > 0 \Rightarrow \begin{cases} V_{BE1} > V_{BB}/2 \Rightarrow Q_1 \ \text{ conduce más} \\ V_{EB2} < V_{BB}/2 \Rightarrow Q_2 \ \text{ se corta} \end{cases} \\ V_L = V_I + \underbrace{V_{BB}/2 - V_{BE1}}{\approx 0} \approx V_I \\ i_L = i{cn} - i_{cp} = i_{cn} \quad \text{saliente} $$
Ciclo negativo
$$ V_I < 0 \Rightarrow \begin{cases} V_{BE1} < V_{BB}/2 \Rightarrow Q_1 \ \text{ se corta} \\ V_{EB2} > V_{BB}/2 \Rightarrow Q_2 \ \text{ conduce más} \end{cases} \\ V_L = V_I - \underbrace{V_{BB}/2 + V_{EB2}}{\approx 0} \approx V_I \\ i_L = -i{cp}\quad \text{entrante} $$
Clase B realimentado
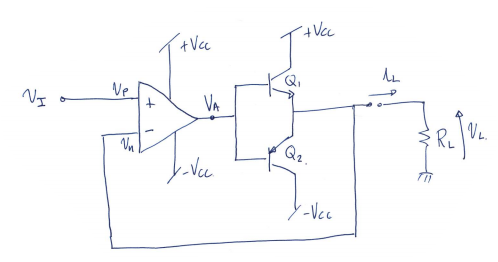
Las características del amplificador operacional son las siguientes: $$ A_{vd} = 10^6 \ V/V \\ R_{id} = \infty \\ R_0 = 0 $$
Las características del circuito son las siguientes: $$ V_{BE1} = V_{EB2} = 0.7 \ V $$
$$ \eta_B = \frac{P_L}{P_{IN}} = \frac{\pi}{4}\cdot \frac{V_L}{V_{CC}} $$
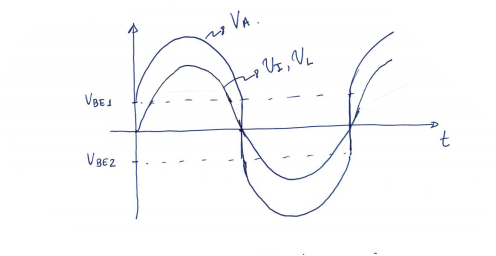
Ciclo positivo
$$ Q_1 \quad \text{en activa} \\ Q_2 \quad \text{cortado} $$
$$ \begin{cases} V_A = A_{vd}(V_p - V_n) = A_{vd}(V_I - V_L) \\ V_A = V_{BE1} + V_L \end{cases} \Rightarrow A_{vd}(V_I - V_L) = V_{BE1} + V_L $$
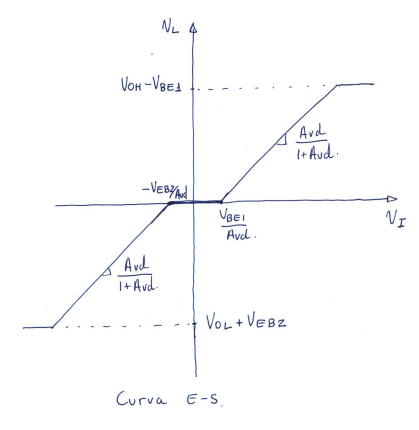
Despejando \(V_L\) llegamos a: $$ V_L = V_I \cdot \frac{A_{vd}}{1 + A_{vd}} - \frac{V_{BE1}}{1+ A_{vd}} $$
$$ V_L = 0 \quad \text{si} \quad V_I = \frac{V_{BE1}}{A_{vd}} = \frac{0.7 \ V}{A_{vd}} = 0.7 \ \mu V $$
Ciclo negativo
$$ Q_1 \quad \text{cortado} \\ Q_2 \quad \text{en activa} $$
$$ \begin{cases} V_A = A_{vd}(V_p - V_n) = A_{vd}(V_I - V_L) \\ V_A = -V_{EB2} + V_L \end{cases} \Rightarrow A_{vd}(V_I - V_L) = -V_{EB2} + V_L $$
Despejando \(V_L\) llegamos a: $$ V_L = V_I \cdot \frac{A_{vd}}{1 + A_{vd}} + \frac{V_{EB2}}{1+ A_{vd}} $$
$$ V_L = 0 \quad \text{si} \quad V_I = -\frac{V_{EB2}}{A_{vd}} = -\frac{0.7 \ V}{A_{vd}} = -0.7 \ \mu V \\ V_A = - V_{EB2} = - 0.7 \ V $$
En reposo
Existe una distorsión de cruce si no conduce \(Q_1\) ni \(Q_2\) y \(A_{vd} \neq \infty\):
$$ \frac{V_{BE2}}{A_{vd}} \le V_i \le \frac{V_{BE1}}{A_{vd}} $$
Máxima corriente de salida del AO
Normalmente el último apartado. Nos dan \(\beta\)
$$ V_{L_{max}}^+ = V_{CC} - V_{BE1} \\ I_{L_{max}}^+ = \frac{V_{L_{max}}}{R_L} \\ i_{o_{max}}^+ = i_{b1} = \frac{I_{L{max}}^+}{\beta_1 + 1} $$