Antes de comentar la memoria de la práctica me gustaría destacar que la versión de PSPICE que estoy usando es la 17. Todas mis conclusiones las voy a hacer con los resultados obtenidos con la salida de las simulaciones de PSPICE.

1 - Análisis del AO en lazo abierto

1.a Represente el módulo (dB) y la fase (°) de la salida del AO. Para ello, puede utilizar las sondas vdb y vphase que encontrará en el menú “Markers Mark Advanced". Con estas sondas, se obtienen el módulo (en dB) y la fase (en grados) de la tensión de salida. Mida y comente las pendientes significativas del módulo y la fase. Estime el valor de la ganancia en lazo abierto del operacional, Avd, la frecuencia de corte superior (-3dB), fp, y la frecuencia de transición (ganancia unidad), f

Las condiciones iniciales para este apartado serán:

• Utilizar el integrado AO uA741
• Alimentar el AO con \(V_{+} = + 12 \ V \) y \(V_{-} = -12 \ V\)
• Alimentar la entrada no inversora con un VSIN con \(V_{ac} = 1V\) con AC Sweep que vaya desde \(f = 0,1 \ Hz\) a \(f = 1 \ GHz\).

En base a esto el esquemático será el siguiente:

Para poder representar el módulo y la fáse utilizaremos las sondas \(V_{dB}\)(para el módulo) y \(V_p\)(para la fase) y los conectamos a la salida del operacional. La simulación obtenida es la siguiente, siendo rojo para el diagrama de módulo y verde para el diagrama de fase:

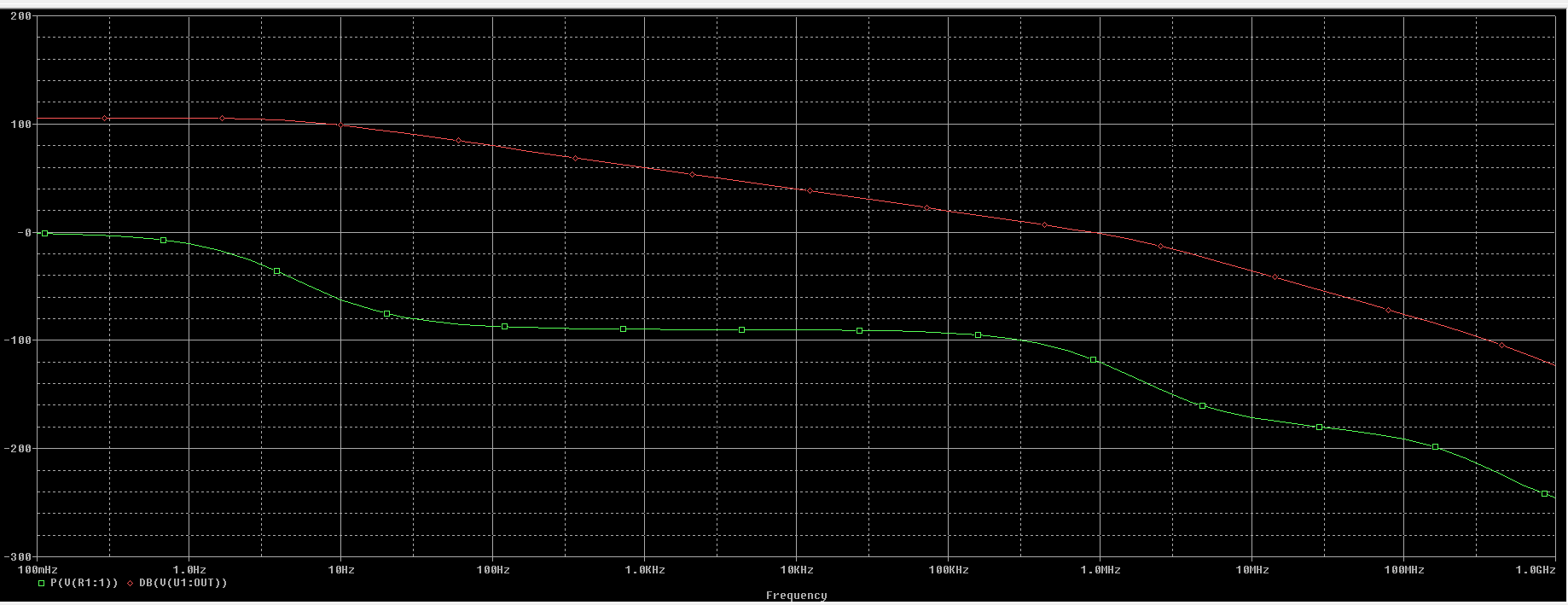
Observando la representación de módulo y de fase podemos determinar que es un filtro paso bajo con 3 polos. Estos polos se encuentran en \(5 \ Hz\), \(1.7 \ MHz\) y \(500 \ MHz\).

Obtenemos las siguientes medidas: $$ A_{vd}= 105 \ dB \qquad \text{Ganancia del lazo abierto del operacional} \\ f_t = 870 \ KHz \qquad \text{Frecuancia de transición cuando la ganancia es 0 dB}\\ f_p = 5.2 \ Hz \qquad \text{Frecuencia de corte superior, la ganancia cae -3 dB}\\ $$

1.b–Ayudándose de la evolución de la fase, estime la frecuencia del segundo polo del amplificador.

La frecuancia del segundo polo se obtendrá observando la representación de fase. \(f_{polo 2} = 1.7 \ MHz\)

1.c –Repita la simulación del punto 1.a utilizando el AO LF411. Ayudándose de los datos de catálogo, comente las principales diferencias encontradas entre ambos operacionales.

Cambiamos el operacione en el circuito de tal forma:

La simulación es la siguiente. Siendo azul el diagrama de módulo (dB) y amarilló el diagrama de fase (grados).

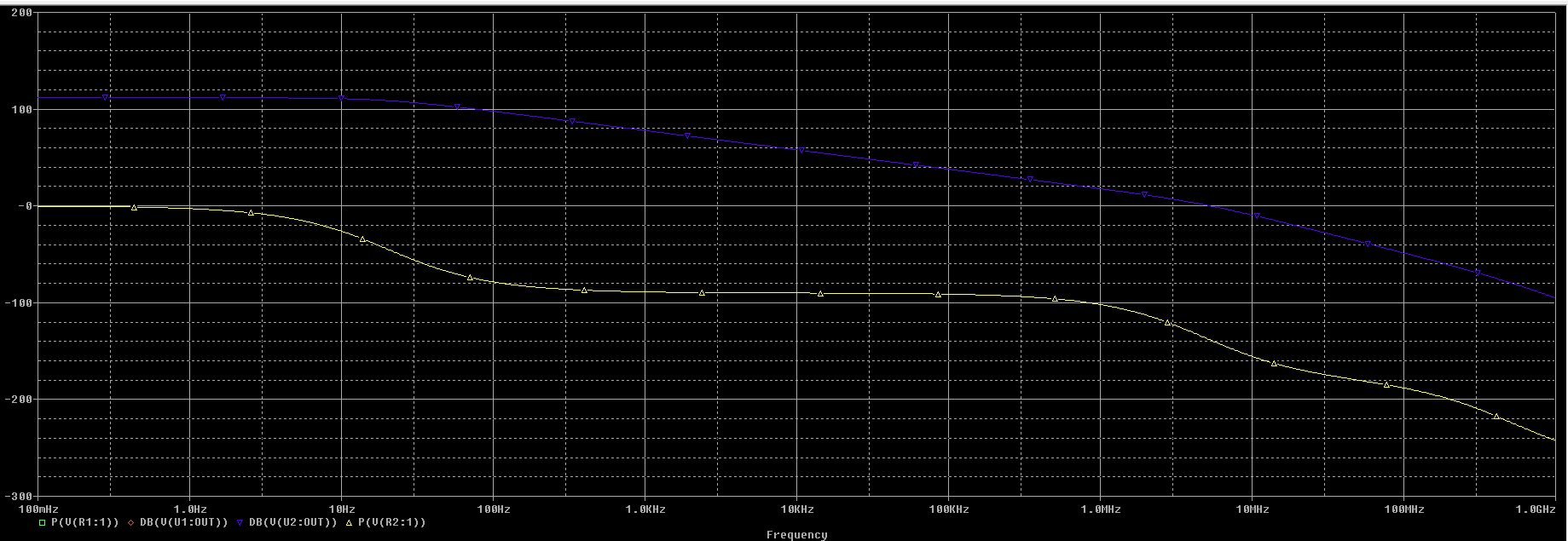
Con el cambio del operacional tendremos que los polos estarán en \(20 \ Hz\), \(4.6 \ MHz\) y \(500 \ MHz\)

Obtenemos las siguientes medidas: $$ A_{vd}= 112 \ dB \qquad \text{Ganancia del lazo abierto del operacional} \\ f_t = 5.2 \ MHz \qquad \text{Frecuancia de transición cuando la ganancia es 0 dB}\\ f_p = 20 \ Hz \qquad \text{Frecuencia de corte superior, la ganancia cae -3 dB}\\ $$ Respecto a las diferencias que hay entre los operacionales mirando el catálogo hay que destacar:

• La resistencia de entrada de UA741 es de 1MΩ y 1TΩ el del LF411.
• El factor GBW de UA741 es de 1MHz y 4 MHz para LF411.
• El factor Slew-rate del LF411 es bastante superior al del UA741. Siendo en el LF411 15 V/us frente a los 0,5 V/us del UA7411.
• El Voltaje de offset del LF411 será 0,8mV y 1mV para el UA741.

Ejercicio 2

2.a-Represente el módulo y la fase de la tensión de salida del seguidor. Estime la frecuencia de corte del seguidor, fH, y el producto GxBW.

Capturamos el esquemático de un seguidor de tensión basado en el uA741. Modificamos la simulación para representar entre \(0,1 \ Hz\) hasta \(100 \ MHz\). Se quedará de la siguiente forma:

La simulación de módulo en color verde (dB) y fase en color rojo(º):

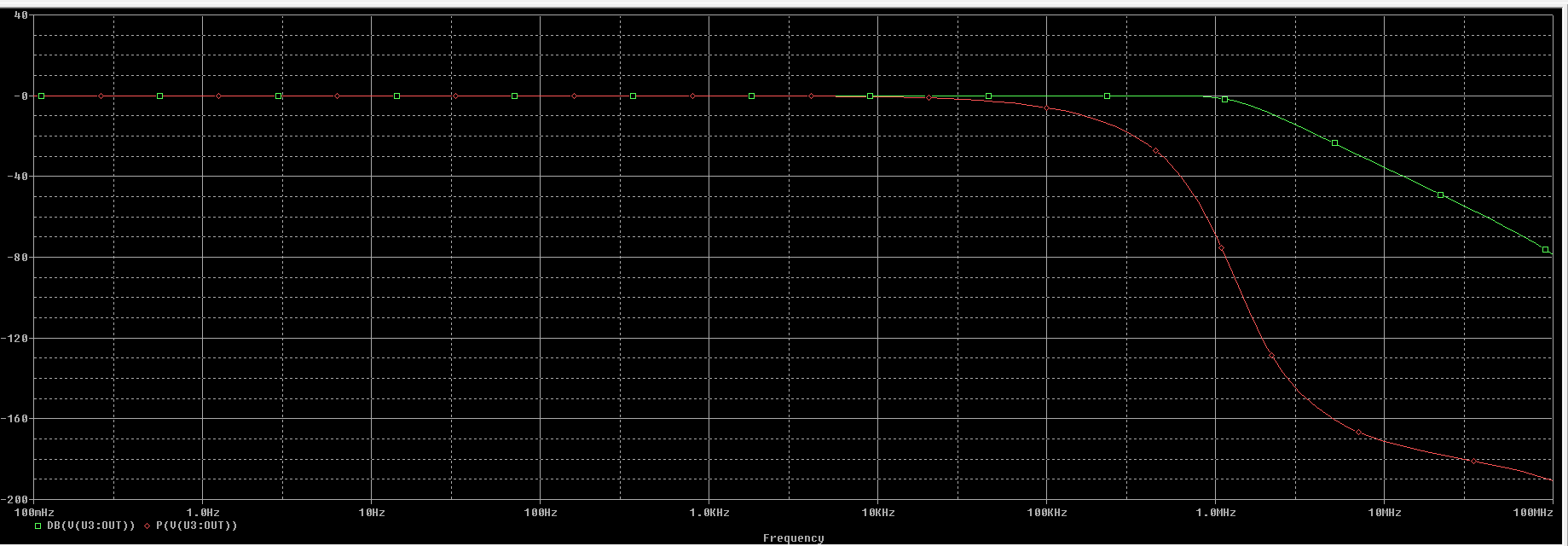
A partir de la gráfica obtenemos lo siguiente: $$ f_{H} = 1.35 \ MHz \\ G \cdot BW = 1 \cdot 1.35 \ MHz = 1.35 \ MHz $$

2.b -Repita la simulación para un amplificador inversor con GV = -1. ¿Se conserva el producto GxBW?

Para lograr un \(G_{V} = -1\) lo hacemos tal que \(R_{1} = 1 \ k\Omega \) y \(R_2 = 1 \ k\Omega\) para que se cumpla \(G_v = - \frac{R_2}{R_1}\). Tendremos un esquemático de la siguiente forma. Notese que en el esquemático \(R_1\) será \(R_4\) y \(R_2\) será \(R_5\):

La gráfica de la simulación es la siguiente. Siendo el color verde para el digrama de módulo en dB y el rojo para el diagrama de fase en grados:

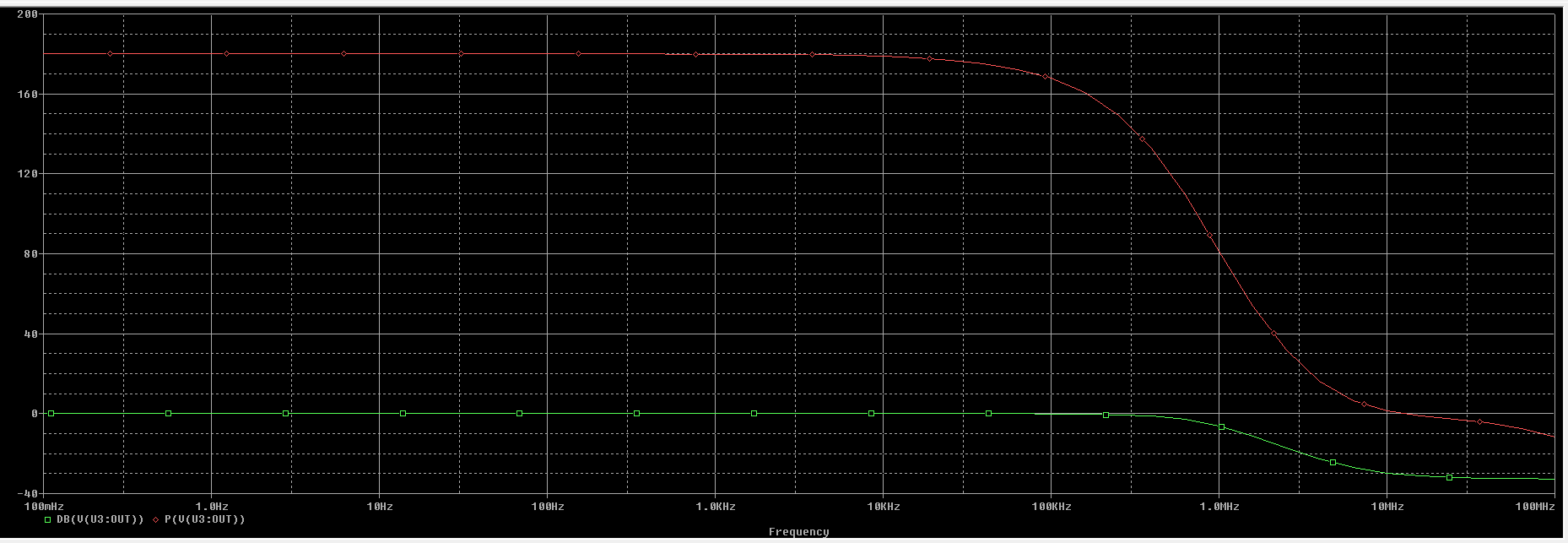
Obtenemos los siguientes resultados: $$ f_{H} = 630 \ KHz \\ G \cdot BW = 1 \cdot 630 \ KHz = 630 \ KHz $$

Con lo que no se conserva el producto.

2.c -SLEW-RATE (SR): Con una señal sinusoidal de VAMPL= 1V en la entrada, obtenga la tensión de salida para: f = 50 kHz, 100 kHz, 500 kHz. Comente los resultados obtenidos en la simulación y estime el valor del SR del modelo utilizado por el PSPICE para el operacional uA741. Calcule el ancho de banda de potencia (Full Power Bandwidth, FPB) y verifique el resultado con la simulación.

Con el mismo esquemático que en el apartado 2a iremos modificando el parámetro de la frecuencia en el generador sinusoidal.

Las gráficas son las siguientes:

f = 50 KHz

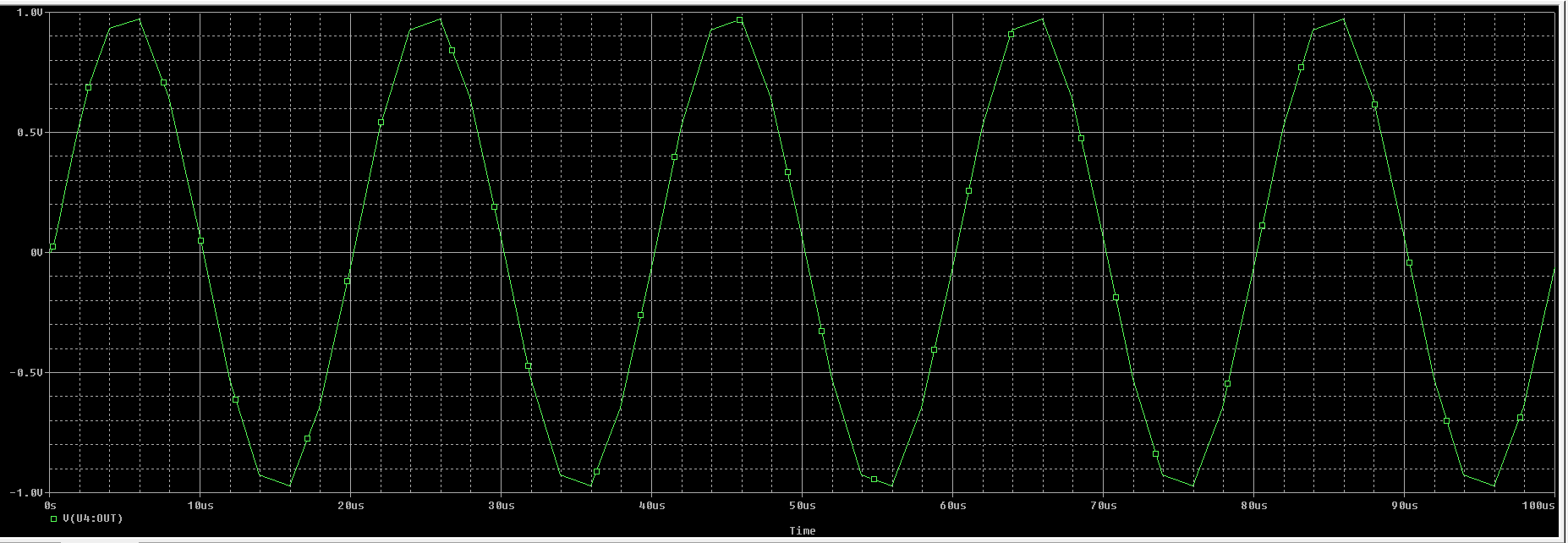
f = 100 KHz

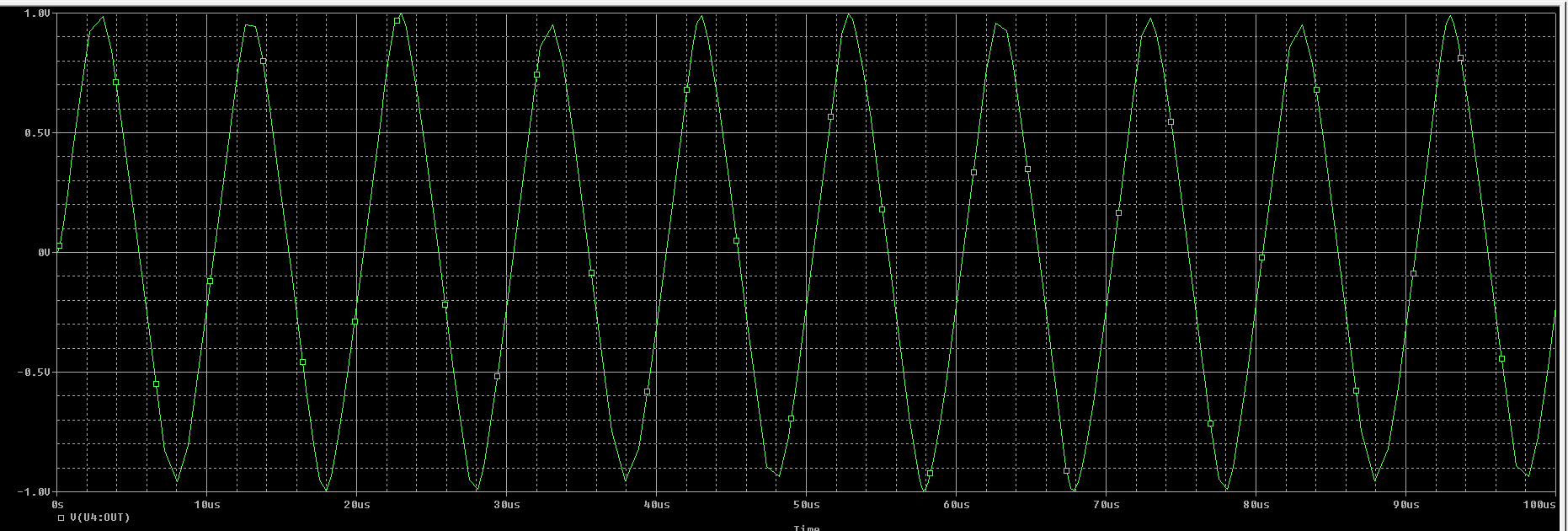
f = 500 KHz

De las simulaciones podemos ver que el dispositivo empieza a distorsionar a partir de \(f = 500 \ KHz\).

SR es el efecto no lineal de los amplificadores. Representa la incapacidad de un amplificador para seguir variaciones rápidas de la señal de entrada. Se le define como la máxima tasa de cambio en el  voltaje de salida cuando el voltaje de entrada cambia.

En las especificaciones de nuestro A741 nos dicen que tiene un \(SR = 0.5 \ V/\mu s\). De la simulación podemos determinar que el dispositivo tiene un \(SR = 0,475 \ V/\mu s\).

Para el cálculo del Full Power Bandwidth: $$ FPB = \frac{SR}{2 \cdot \pi \cdot V_{max}} = \frac{0,475 \cdot \frac{1}{1 \cdot 10^{-6}}}{2 \cdot \pi \cdot 11.6} = 6,52 \ KHz $$

2.d -Máxima corriente de salida del operacional, IOmax Con una señal sinusoidal de VAMPL= 1V en la entrada, f = 1 kHz, cambie la resistencia de carga del seguidor a un nuevo valor RL = 10 Ω. Explique el resultado obtenido, y estime la máxima corriente de salida del modelo del amplificador operacional.

El esquemático será el siguiente:

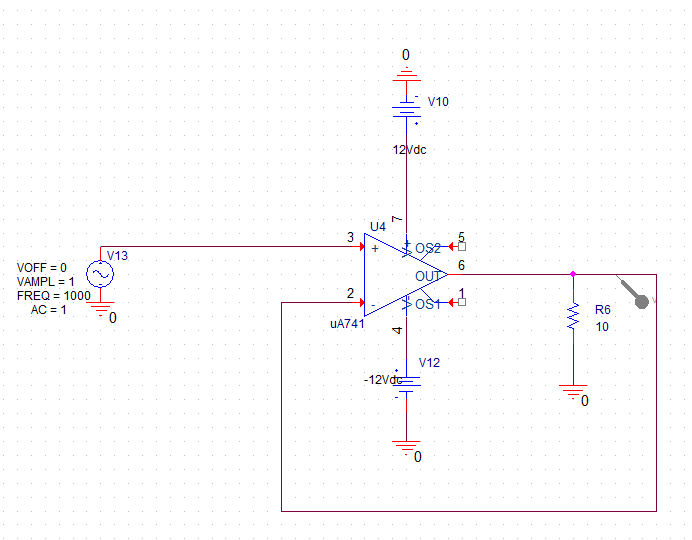
La simulación es la siguiente:

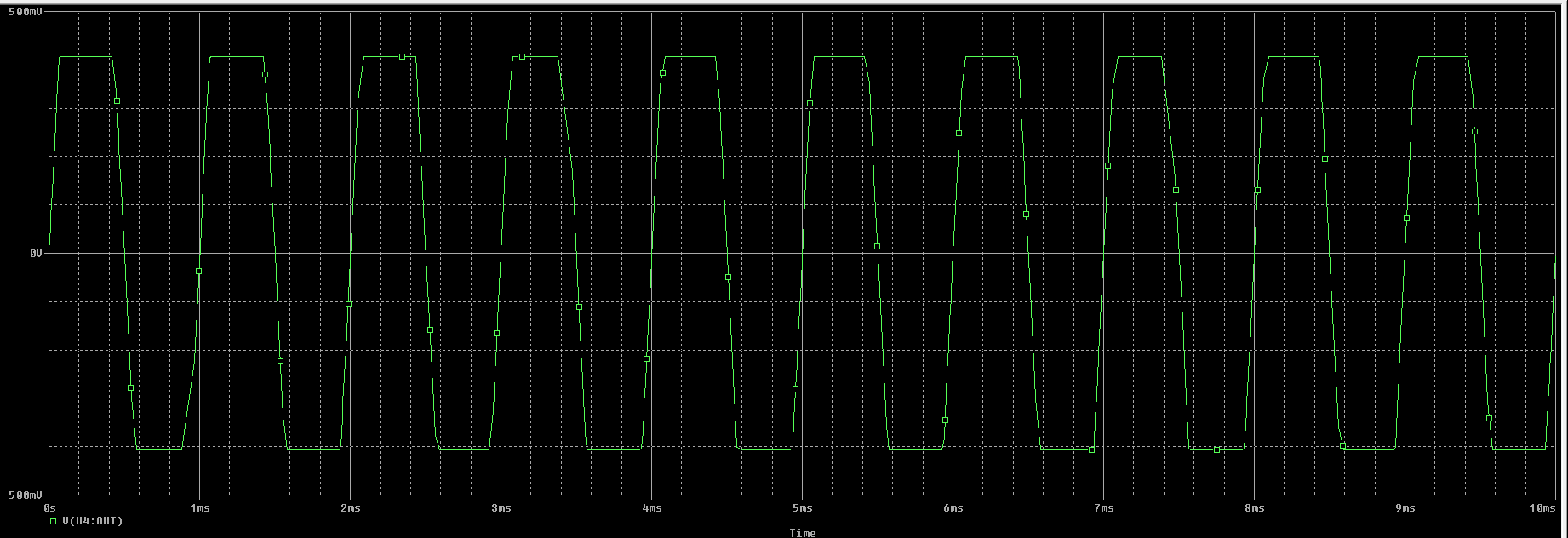
Podeemos ver en la salida que se está saturando. Podemos determinar la máxima corriente de salida de la siguiente forma:

$$ I_{Omax} = \frac{V_{oAO}}{R_L} = \frac{0.406 \ V}{10 \ \Omega} = 0.0406 \ A = 40.6 \ mA $$

Ejercicio 3

3.a -Represente el módulo y la fase de la ganancia de tensión del amplificador. Obtenga la frecuencia de corte superior fH, y el producto GxBW. Compare con los valores teóricos esperados.

El esquemático es el siguiente:

La simulación de módulo (azul en dB) y fase (amarillo en grados) es la siguiente:

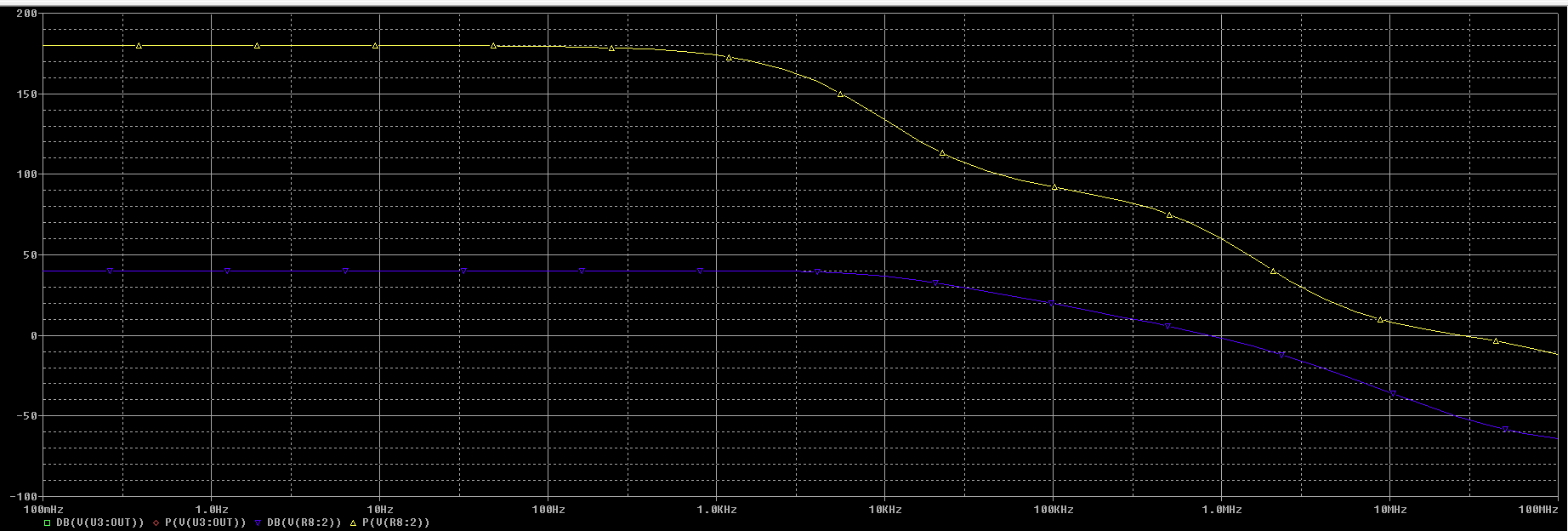
De la que podemos destacar: $$ f_{H} = 9,4 \ KHz \\ G \cdot BW = 100 \cdot 9,4 \ KHz = 940 \ KHz $$

El valor teórico esperado lo sacamos del resultado anterior del ejercicio 1.a. La ganancia \(A_{vd} = 105 \ dB = 10^{\frac{105}{20}}\) y \(f_c = 5,3 \ Hz\). El valor teórico será: $$ G \cdot BW = 10^{\frac{105}{20}} \cdot 5,3 \ Hz = 942.48 \ KHz $$

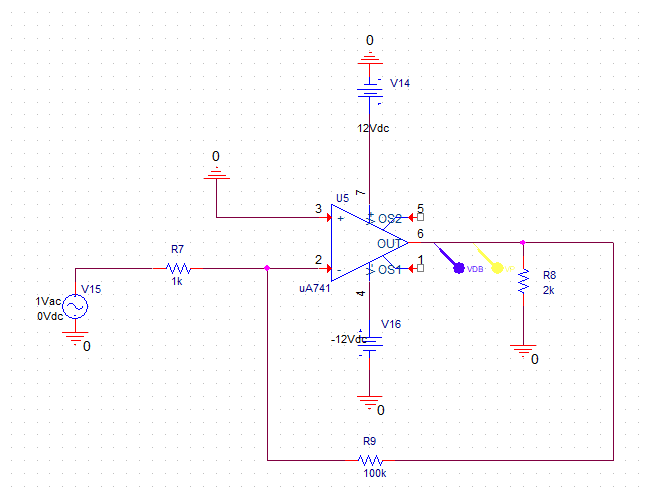
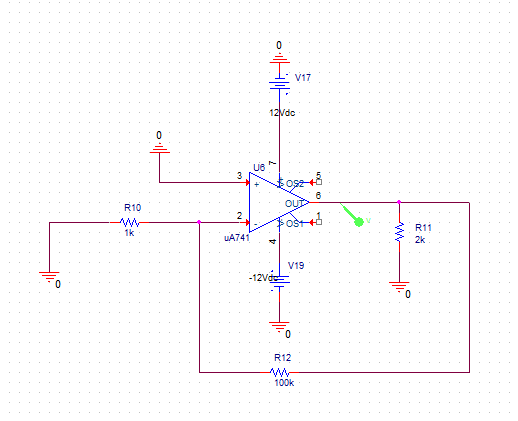
3.b -En este apartado estimaremos el efecto producido por las corrientes de polarización y offset (IB, IOS) en la salida del amplificador diseñado con Gv = -100 V/V. Anulando el generador de entrada, obtenga el error DC en la salida. Repita colocando una resistencia Rp del valor adecuado en la entrada no inversora. Con ambos valores, estime el valor de la corriente IOS del modelo del operacional.

En el primer caso hacemos el esquemático sin la resistencia \(R_p\):

En el segundo caso, pondremos la resistencia \(R_p = \frac{R_1 \cdot R_2}{R_1 + R_2} = 990 \ \Omega\) con el siguiente esquemático. Notese en el esquemático que \(R_1\) será \(R_17\) y \(R_2\) será \(R_16\):

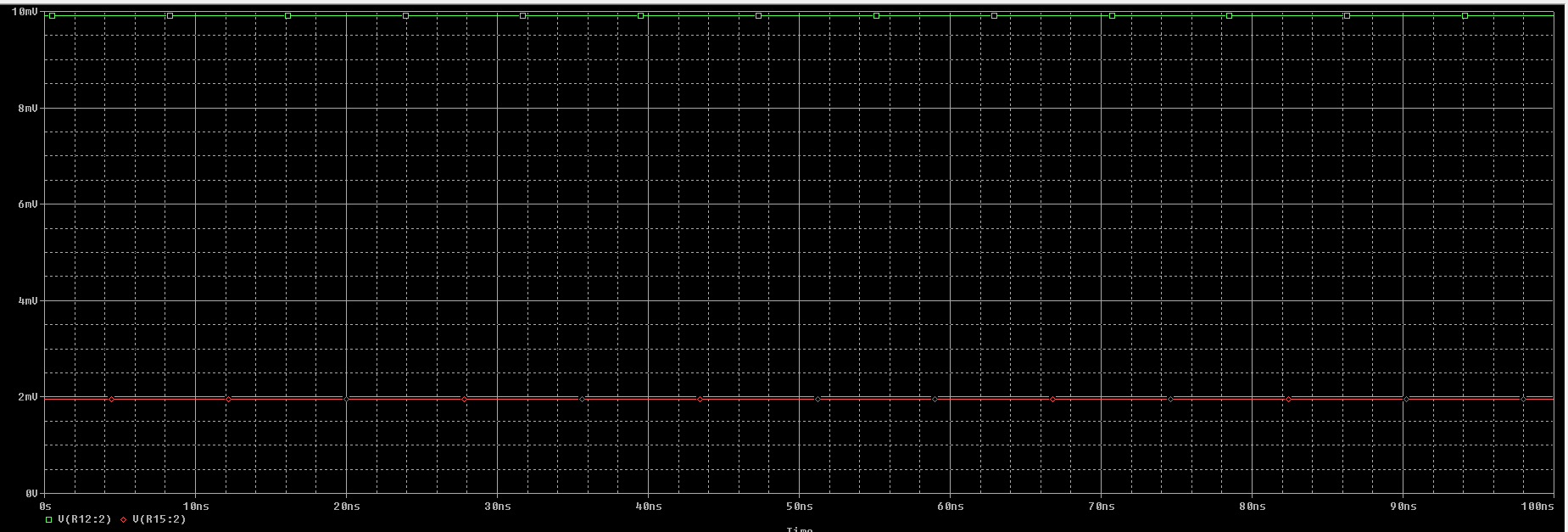
La simulación de los dos esquemáticos es la siguiente. Siendo el la gráfica de color verde para el circuito sin \(R_p\) y en rojo para el esquemático de \(R_p\).

Para calcular el valor de \(I_{OS}\): $$ I_{OS} = I_P - I_N \\ E_{O,IB} = E_{O,IN} + E_{O,IP} = \big ( 1 + \frac{R_1}{R_2}) \cdot [\big ( \frac{R_1 \cdot R_2}{R_1 + R_2}) \cdot I_N - I_p \cdot R_P ] = \\ (1 + \frac{R_2}{R_1}) (R_1 // R_2) [I_N - I_P] = - (1 + \frac{R_2}{R_1}) \cdot (R_1 // R_2) \cdot I_{OS} = - R_2 \cdot I_{OS} $$

Observando la gráfica podemos determinar que \(E_{O,1B} = 1,947 \ mV\) y \(R_1 = 1 \ k \Omega, \ R_2 = 100 \ k \Omega\): $$ I_{OS} = -19,47 \ nA \\ $$ Concluimos con lo siguiente.

$$ E_{0,IB} \lvert_{R_p = 0} = 9,91 \ mV = R_2 \cdot I_N \Rightarrow I_N = 99,15 \ nA \\ I_P = I_{OS} + I_N = 79,68 \ nA \Rightarrow I_B = \frac{I_P + I_N}{2} = \frac{99,15 + 79,68}{2} = 89,415 \ nA $$

Ejercicio 4

4.a -Utilizando los valores R1 = R3 = 1 kΩ, R2 = R4 = 50 kΩ y el AO LF411, obtenga el valor de las ganancias para el modo diferencial y común (Adm, Acm), y el factor de rechazo al modo común, CMRRdB en baja frecuencia. Compare el resultado con los valores especificados por el fabricante en el catálogo para el LF411. Para ello, realice el análisis AC con señal sinusoidal entre 0.1 Hz y 10 MHz con excitación en modo común y en modo diferencial

El circuito en modo diferencial:

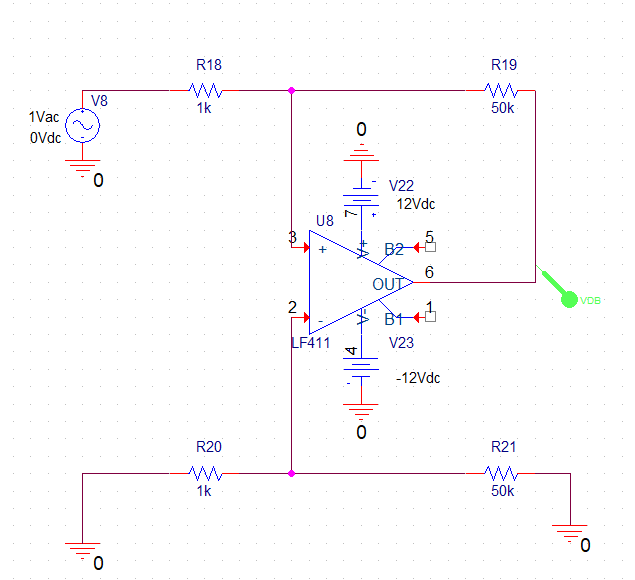
El circuito en modo común:

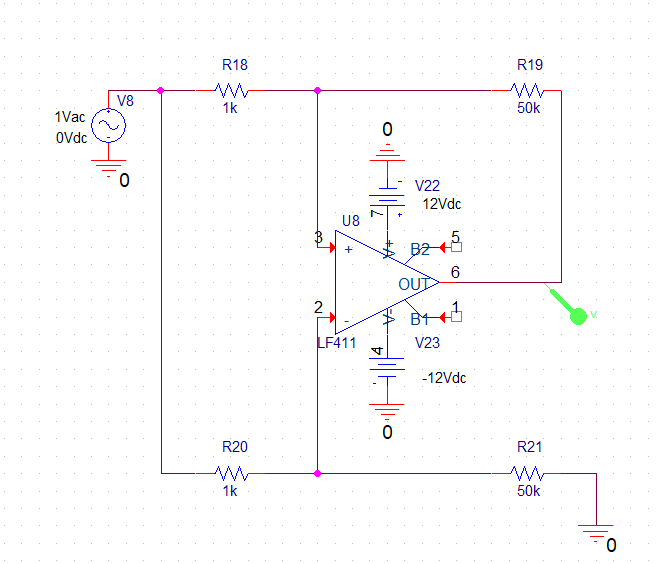
La función de transferencia de nuestro circuito será: $$ V_o = \frac{R_2}{R_1} \cdot (V_2 - V_1) $$

Para calcular el CMRR utilizamos: $$ CMRR = 20 \cdot \log (\frac{A_{dm}}{A_{cm}}) $$

Simulación en modo diferencial:

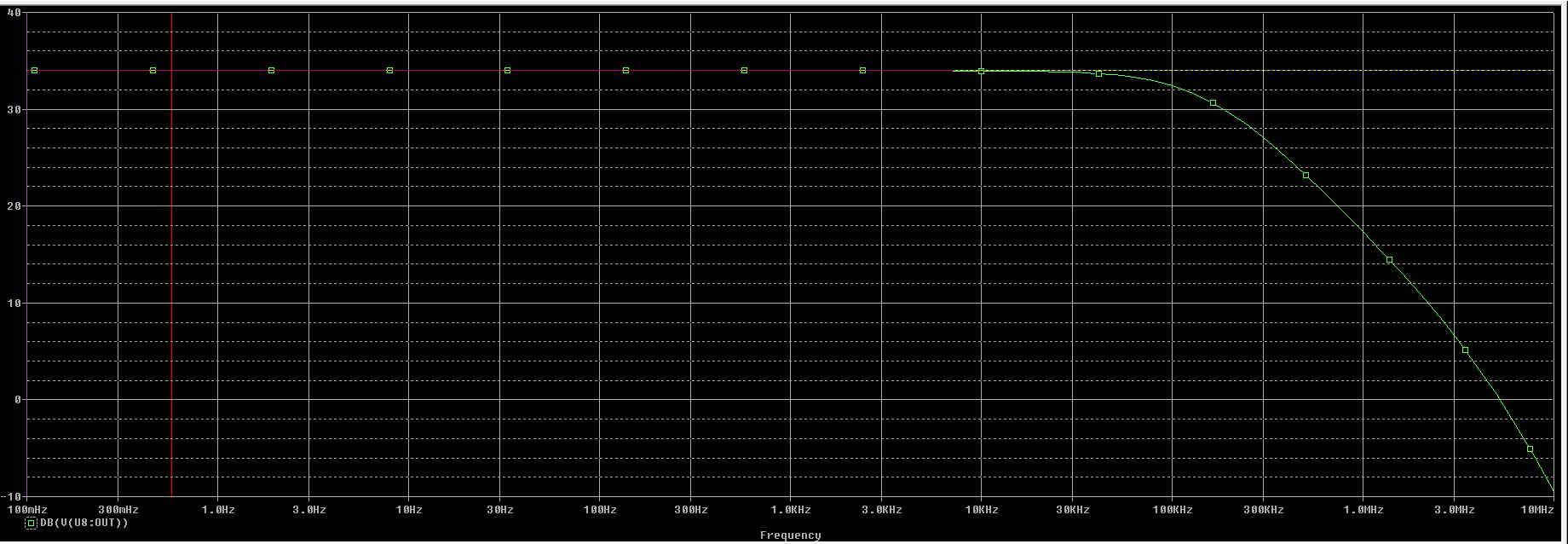
Simulación en modo común:

Para bajas frecuencias: $$ A_{dm} = 33.98 \ dB\\ A_{cm} = -72.08 \ dB $$

Con lo que: $$ CMRR = 20 \cdot \log (\frac{A_{dm}}{A_{cm}}) = 33 - (-72) = 106.06 \ dB $$

4.b -Repita el apartado anterior, suponiendo ahora que se utilizan resistencias con una precisión del 1%, y que estamos en el caso peor. Realice la simulación utilizando el modelo de amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V, (donde solo debería afectar el desapareamiento de las resistencias) y con el LF411, (donde el efecto del desapareamiento de las resistencias se suma al del CMRR propio del operacional).

Como en el enunciado nos dicen que las resistencias tienen un error de un 1% y estamos en el peor escenario, el valor de las resistencias será el siguiente:

La primera opción de resistencias sería la siguiente: $$ \frac{R_{1max}}{R_{2min}} = \frac{R_{3min}}{R_{4max}} \Rightarrow \\ R_{2min} = 49500 \ \Omega \\ R_{3min} = 990 \ \Omega \\ R_{4max} = 50500 \ \Omega \\ R_{1max} = 1010 \ \Omega $$

La segunda opción de resistencias será la siguiente: $$ \frac{R_{1min}}{R_{2max}} = \frac{R_{3max}}{R_{4min}} \Rightarrow \\ R_{2max} = 50500 \ \Omega \\ R_{3max} = 1010 \ \Omega \\ R_{4min} = 49500 \ \Omega \\ R_{1min} = 990 \ \Omega $$

Nos piden en el ejercicio simular el circuito en modo común y modo diferencia usando el amplificador operacional cuasi-ideal OPAMP y con el operacional LF411.

Modo común con la primera opción de resistencias

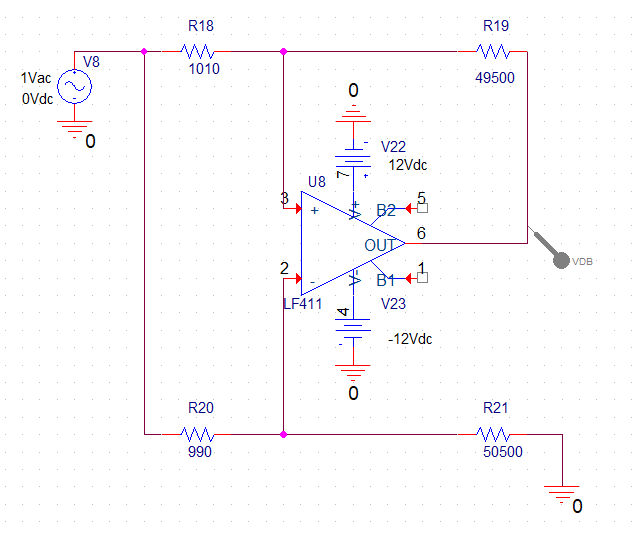
Esquemático de modo común con la primera opción de resistencias usando el operacional LF411.

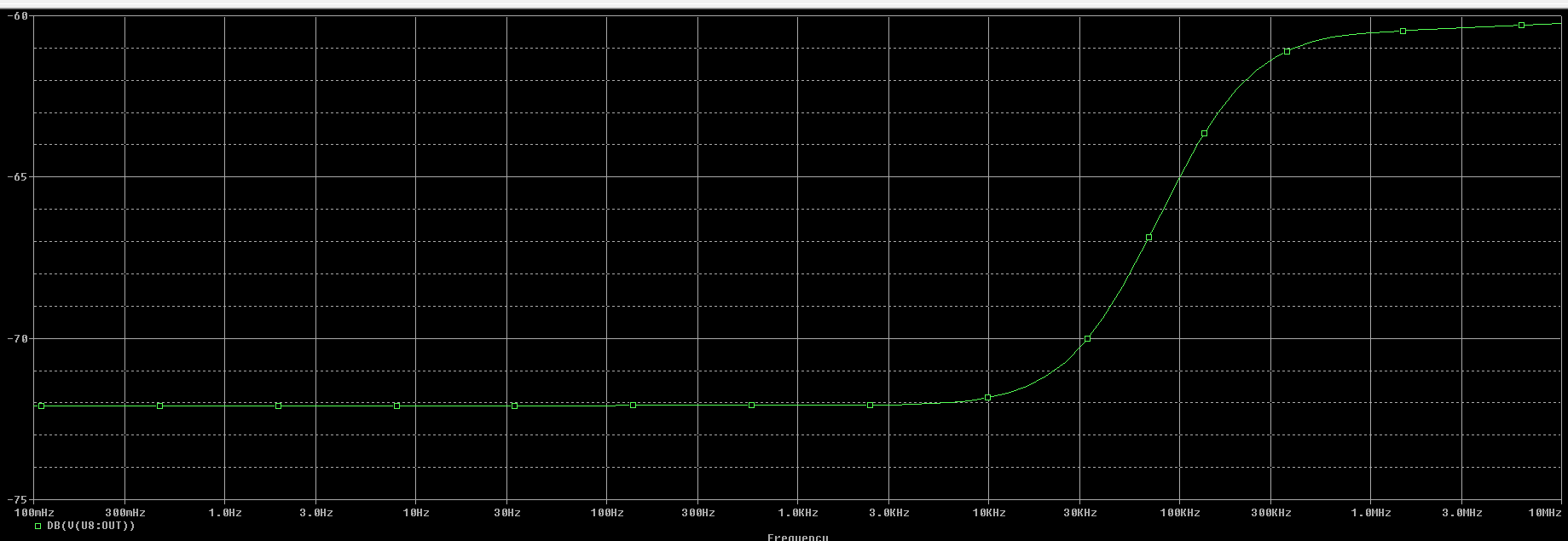
Gráfica de la simulación de la salida en modo común de la primera opción de resistencias usando el operacional LF411.

En la gráfica podemos observar que para baja frecuencia obtendremos: $$ A_{cm_{LF411}} = -28,2 \ dB $$

Esquemático de modo común con la primera opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

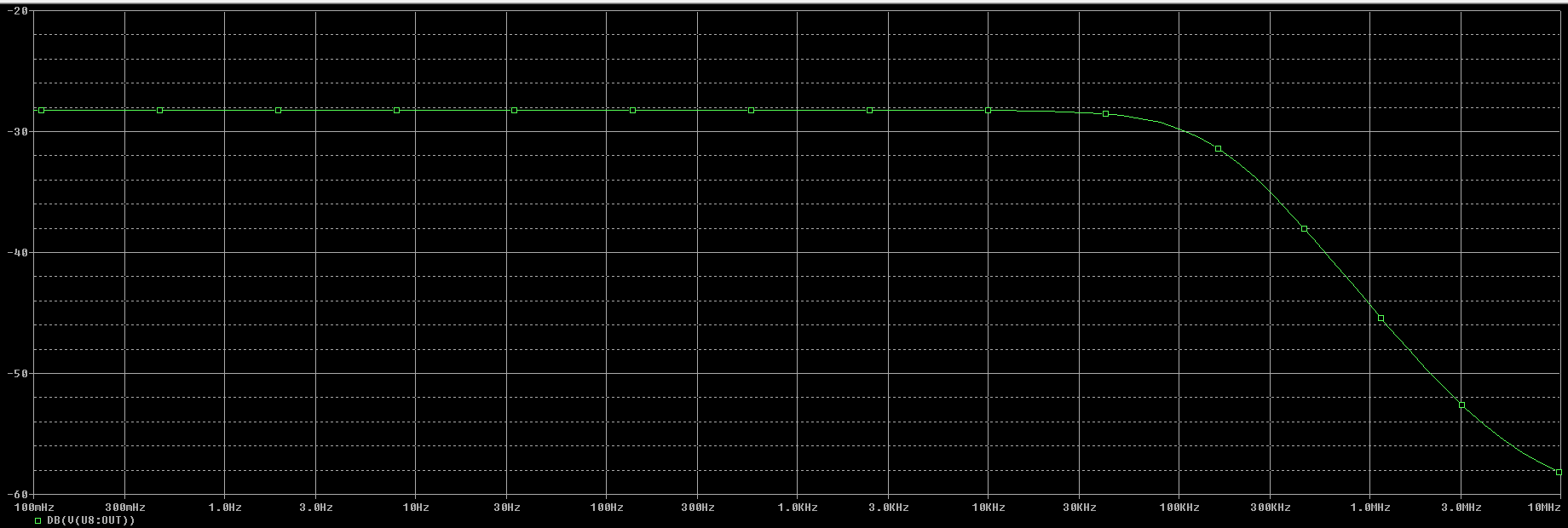
Gráfica de modo común de la salida con la primera opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

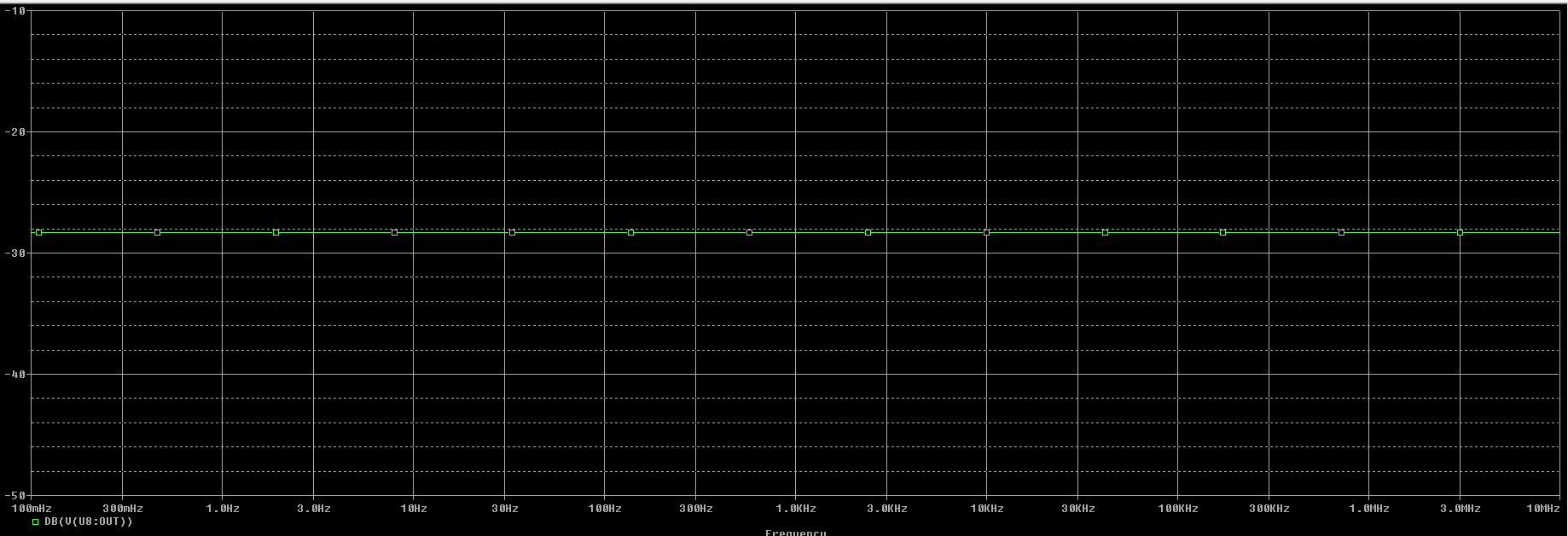
Podemos observar en la gráfica que: $$ A_{cm_{OPAMP}} = -28,3 \ dB $$

Modo común con la segunda opción de resistencias

Esquemático de modo común con la segunda opción de resistencias usando el operacional LF411.

Gráfica de la simulación de la salida en modo común de la segunda opción de resistencias usando el operacional LF411.

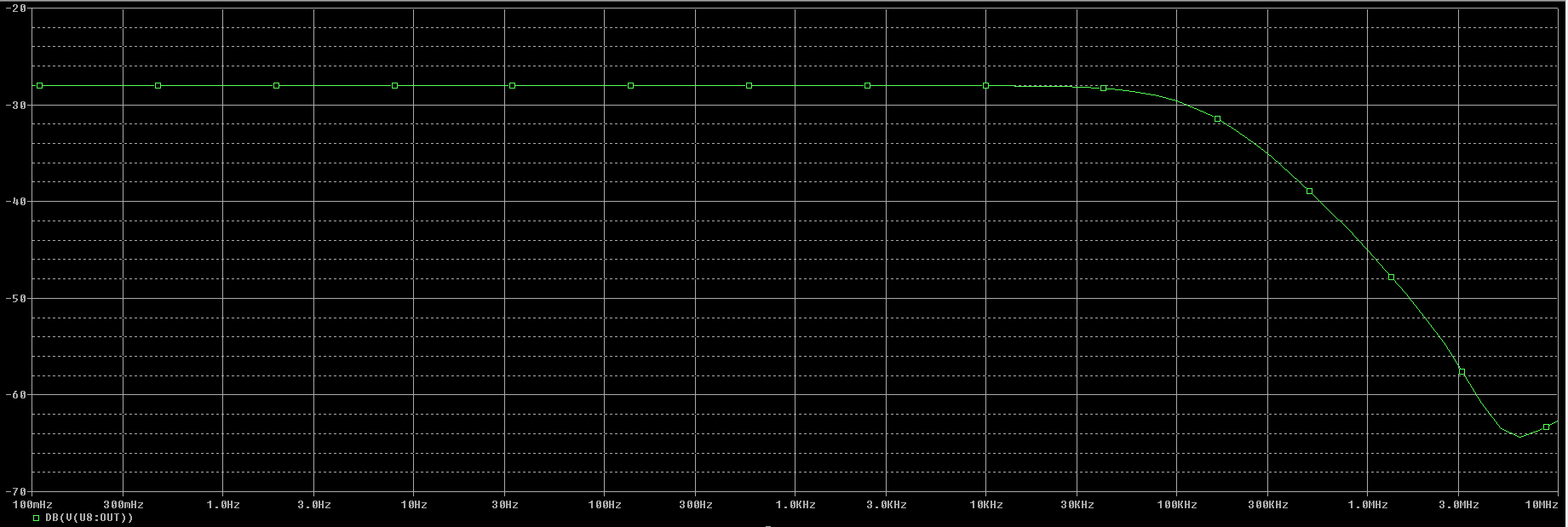
En la gráfica podemos observar que para baja frecuencia obtendremos: $$ A_{cm_{LF411}} = -28,0 \ dB $$

Esquemático de modo común con la segunda opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

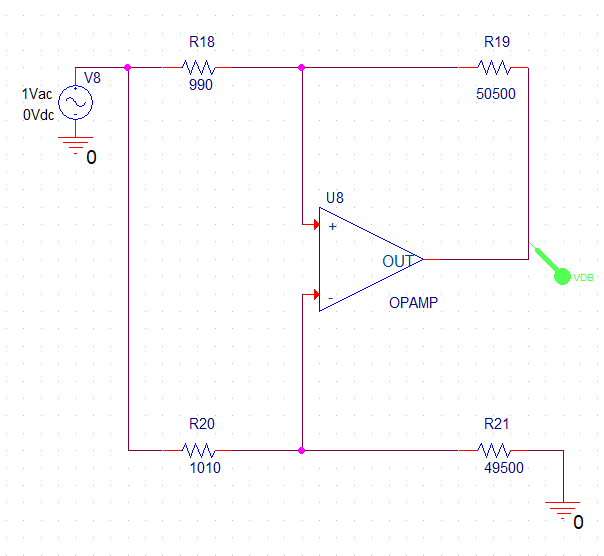
Gráfica de modo común de la salida con la segunda opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

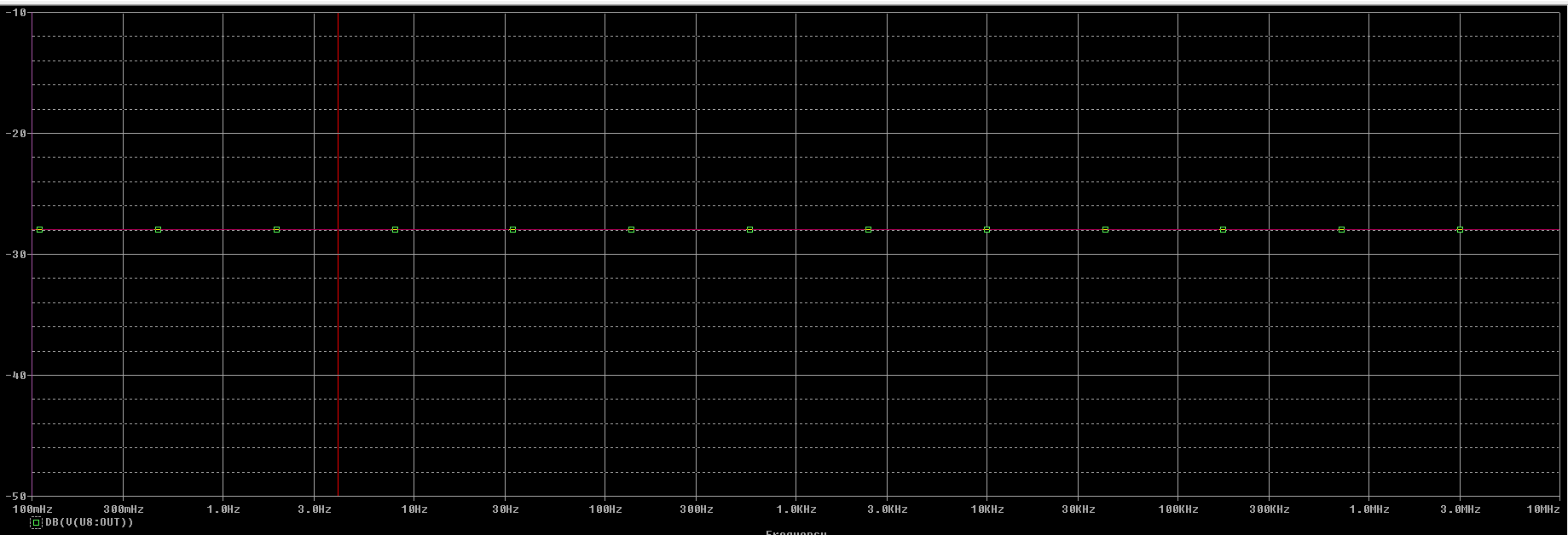
Podemos observar en la gráfica que: $$ A_{cm_{OPAMP}} = -28,0 \ dB $$

Modo diferencial con la primera opción de resistencias

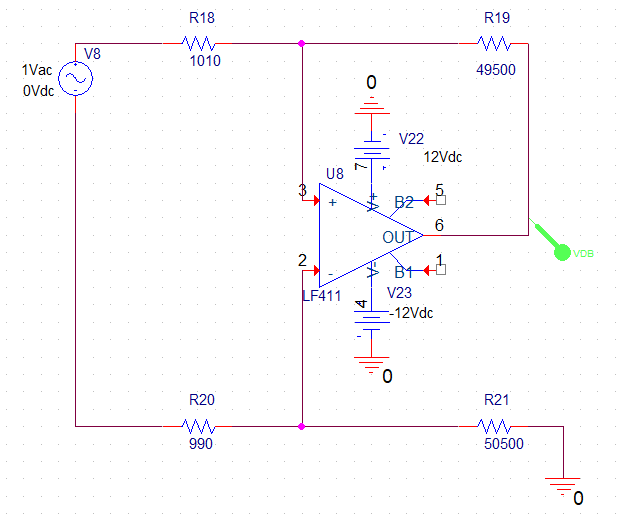
Esquemático de modo diferencial con la primera opción de resistencias usando el operacional LF411.

Gráfica de la simulación de la salida en modo diferencial de la primera opción de resistencias usando el operacional LF411.

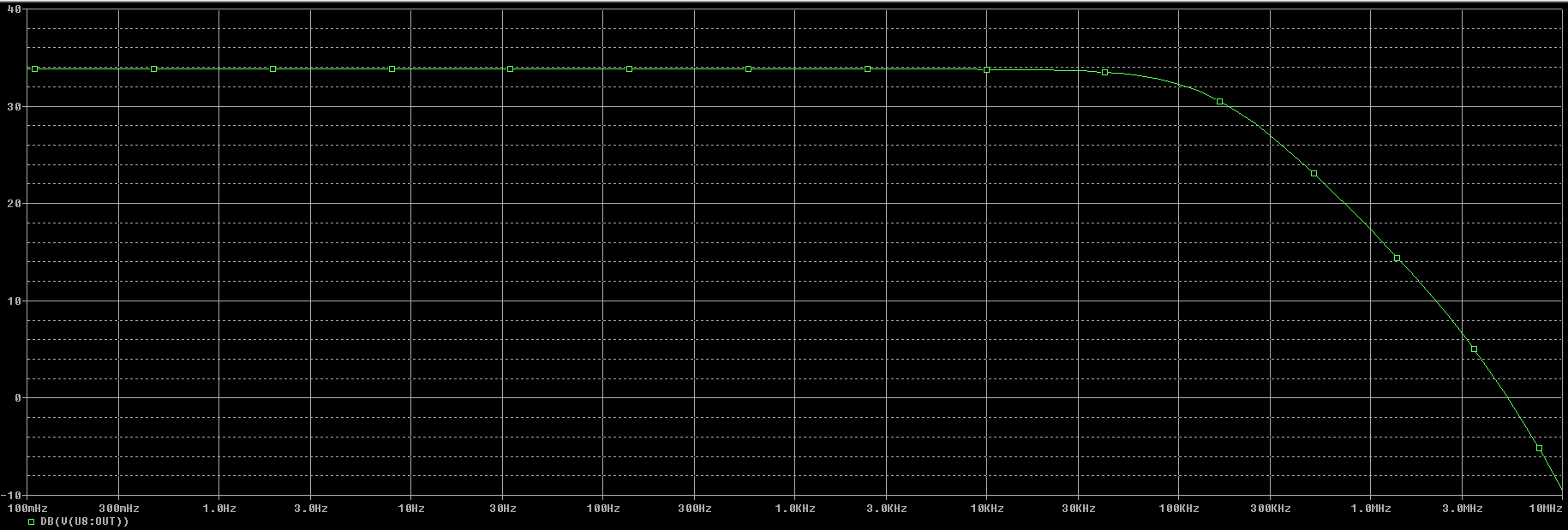
En la gráfica podemos observar que para baja frecuencia obtendremos: $$ A_{dm_{LF411}} = 33,98 \ dB $$

Esquemático de modo diferencial con la primera opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

Gráfica de modo diferencial de la salida con la primera opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

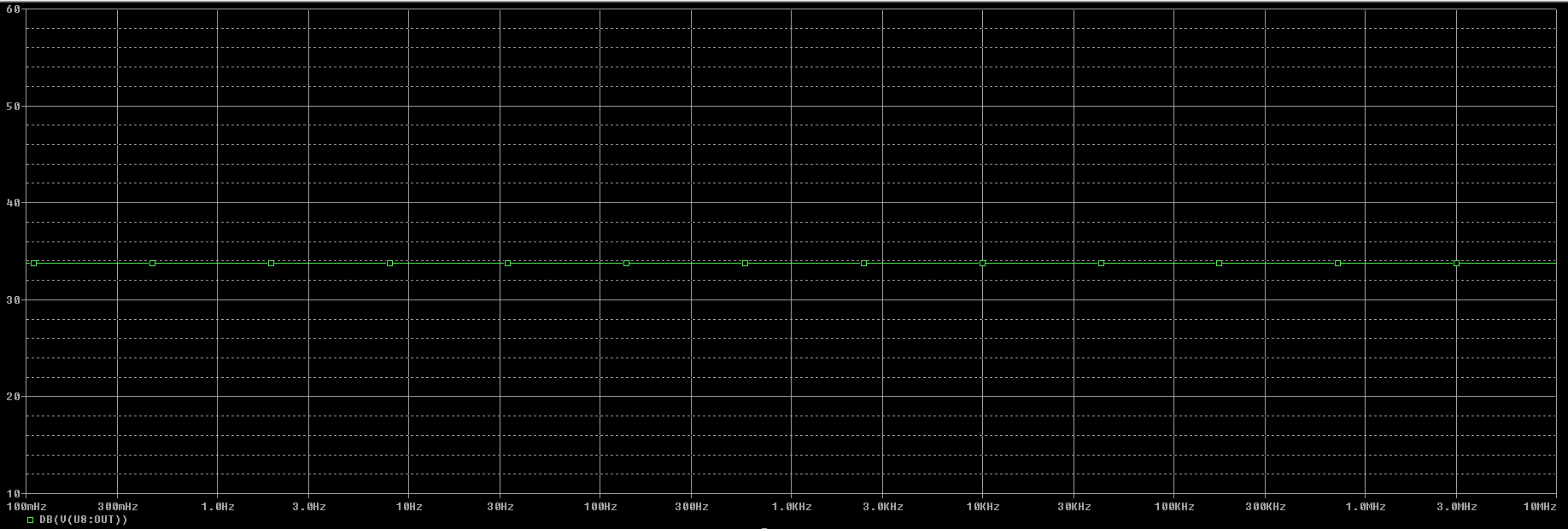
Podemos observar en la gráfica que: $$ A_{dm_{OPAMP}} = 33,98 \ dB $$

Modo diferencial con la segunda opción de resistencias

Esquemático de modo diferencial con la segunda opción de resistencias usando el operacional LF411.

Gráfica de la simulación de la salida en modo diferencial de la segunda opción de resistencias usando el operacional LF411.

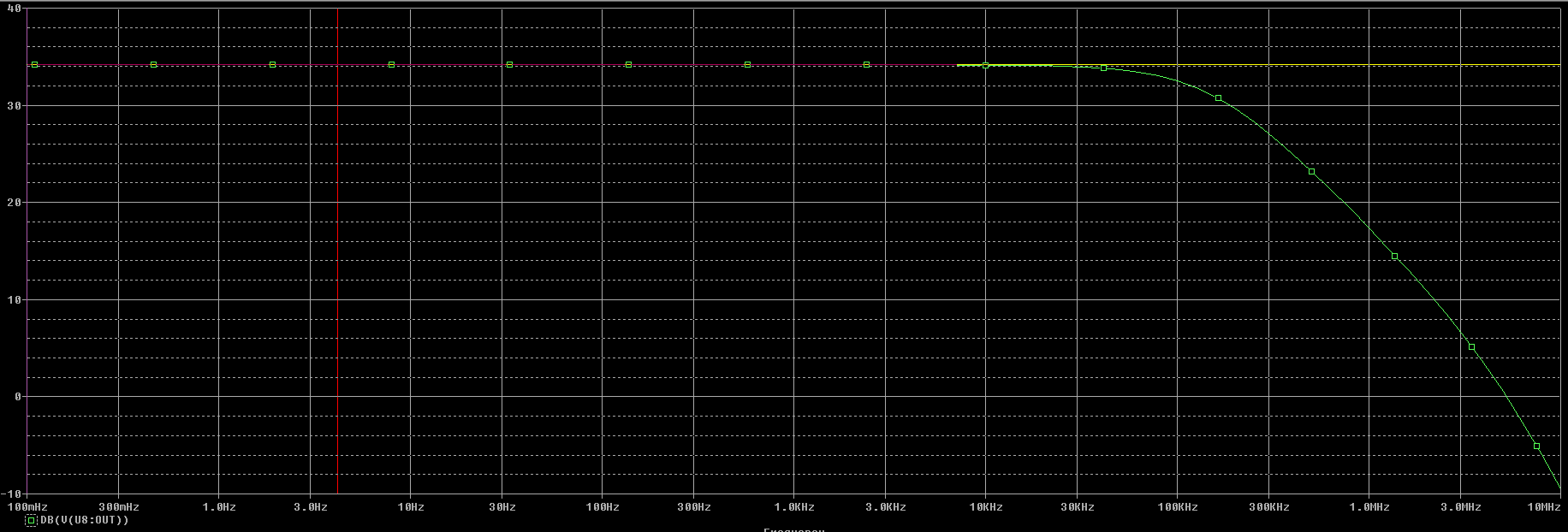
En la gráfica podemos observar que para baja frecuencia obtendremos: $$ A_{dm_{LF411}} = 33,982 \ dB $$

Esquemático de modo diferencial con la segunda opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

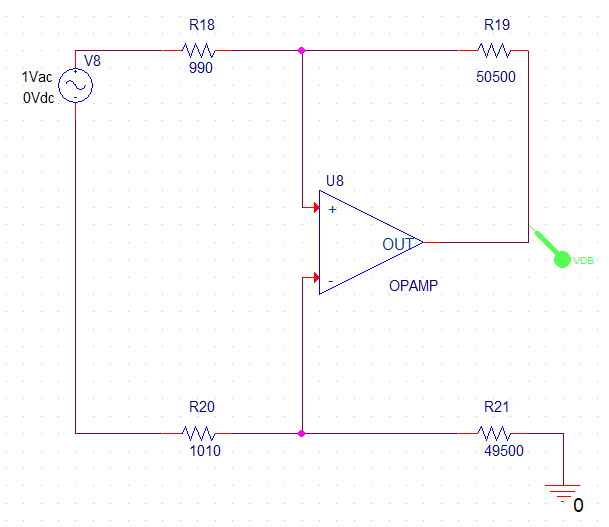
Gráfica de modo diferencial de la salida con la segunda opción de resistencias usando el amplificador operacional cuasi-ideal OPAMP con ganancia GAIN=1E6 V/V.

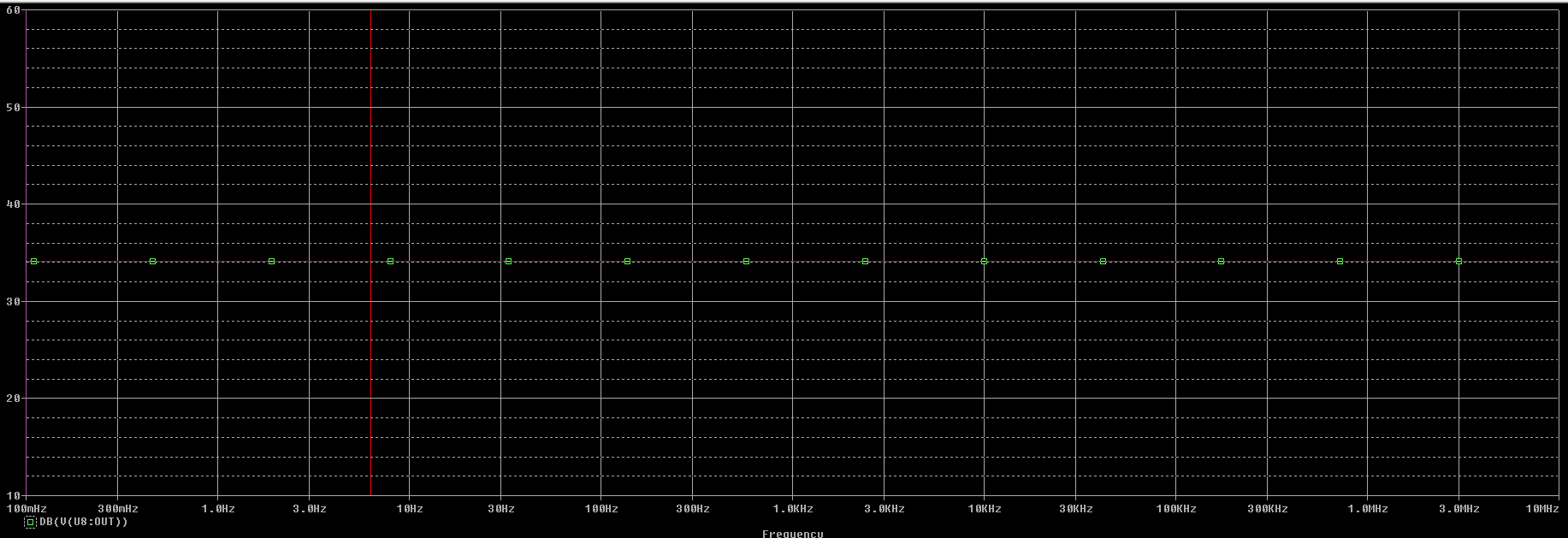
Podemos observar en la gráfica que: $$ A_{dm_{OPAMP}} = 33,98 \ dB $$

Comparación de los diferentes casos

Finalmente el cáculo del CMRR para todos los casos es el siguiente: $$ CMRR_{LF411_{caso1}} = 20 \cdot \log{\frac{A_{dm}}{A_{cm}}} = 33,98 - (-28,2) = 62,18 \ dB \\ CMRR_{OPAMP_{caso1}} = 20 \cdot \log{\frac{A_{dm}}{A_{cm}}} = 33,98 - (-28,3) = 62,28\ dB \\ CMRR_{LF411_{caso2}} = 20 \cdot \log{\frac{A_{dm}}{A_{cm}}} = 34,982 - (-28,0) = 61,982 \ dB \\ CMRR_{OPAMP_{caso2}} = 20 \cdot \log{\frac{A_{dm}}{A_{cm}}} = 33,98 -(-28,0) = 61,98 \ dB \\ $$ Podemos observar que la peor situación es para la primera opción de resistencias. Cambiar las resistencias ha supuesto un cambio grande pues hemos pasado de tener un CMRR de 106.06 dB a tener un CMRR en torno a 62 dB.

Ejercicio 5- Evolución de las impedancias de entrada y salida con la frecuencia

5.a -Con el uA741 en lazo abierto, obtenga el valor de sus impedancias de entrada Zid(f) y salida (Zo(f)).

Para el cáculo de \(Z_{id}(f) \) el esquemático es el siguiente:

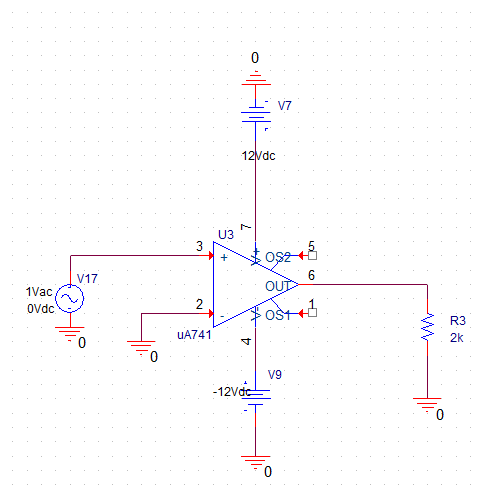
Y la gráfica de \( V(V17:+)/I(V17) \):

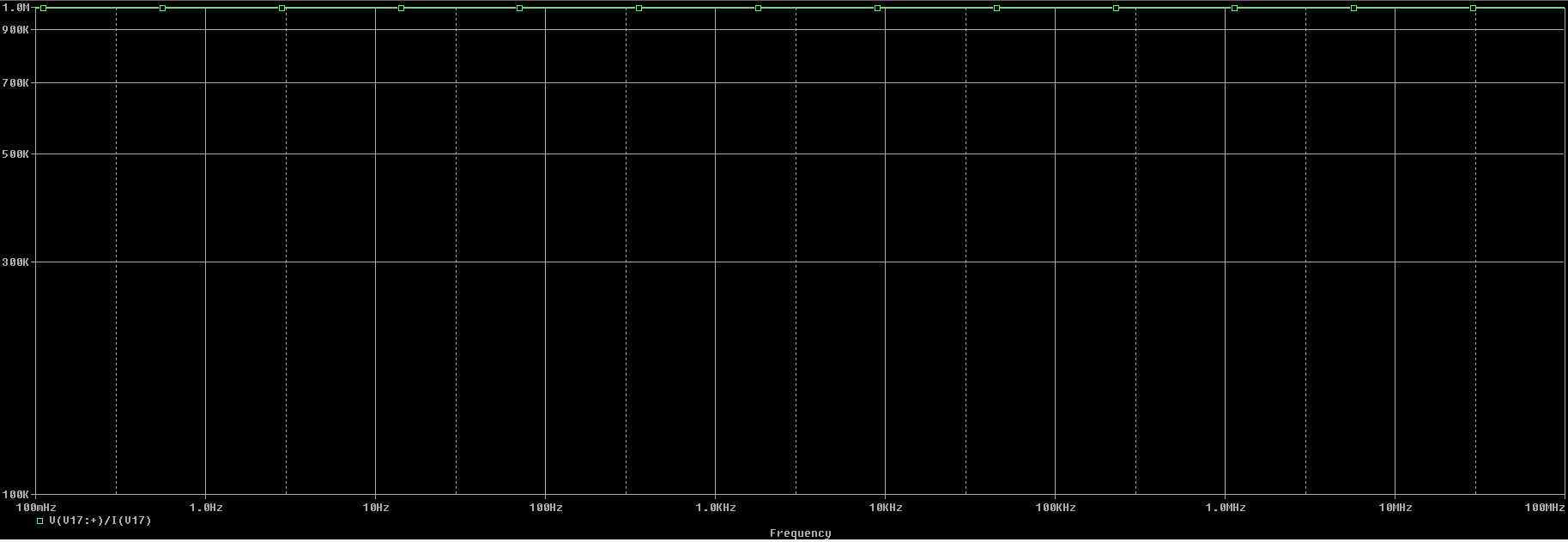
Con lo que: $$ Z_{id} = \frac{V}{I} \approx 1 \ M \Omega $$

Para el cálculo \(Z_o(f)\) el esquemático es el siguiente:

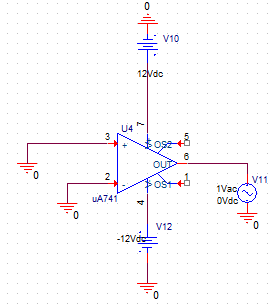
Y la gráfica \( V(V11:+)/I(V11) \)

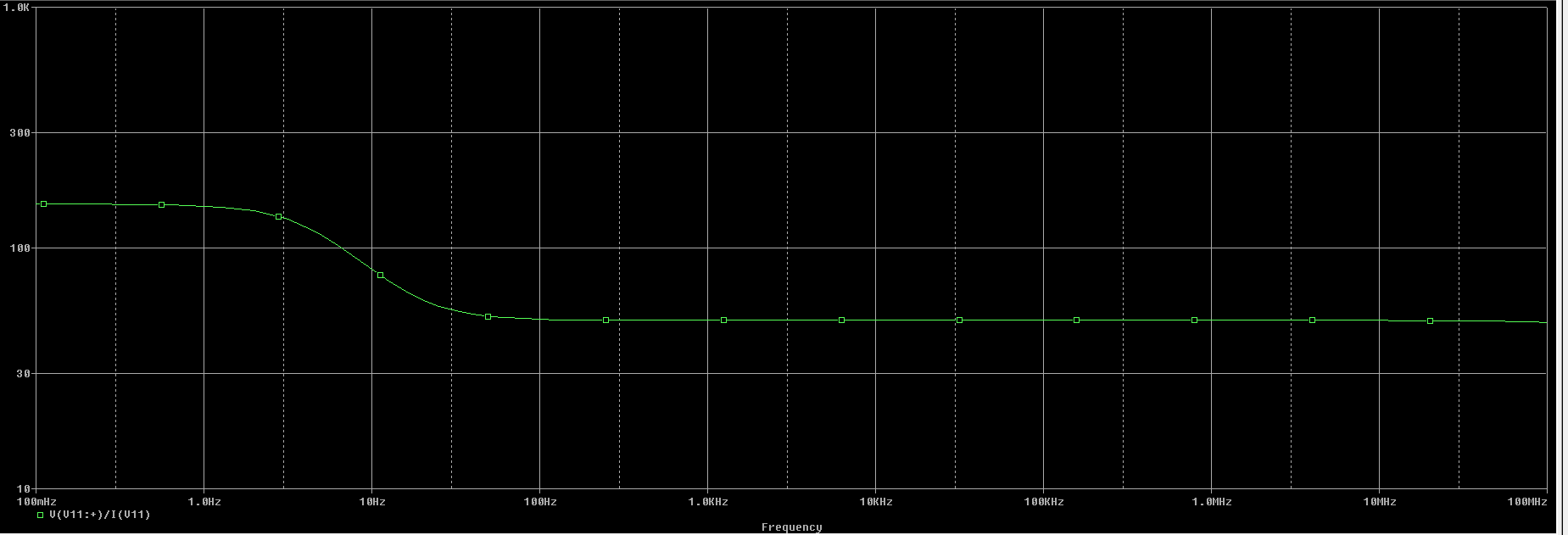
Con lo que obtenemos lo siguiente para baja frecuencia: $$ Z_o= \frac{V}{I} \approx 151,7 \ \Omega $$

5.b -Impedancia de entrada, ZiCR(f): represente en una misma gráfica la evolución de ZiCR(f) para un amplificador realimentado con ganancias GV=1, GV=100 y GV=-100. Incluya la resistencia Rp que minimiza el efecto de las corrientes de polarización. Compare el resultado de la simulación con el valor esperado.

Para \(G_V = 1 \) el esquemático es el siguiente:

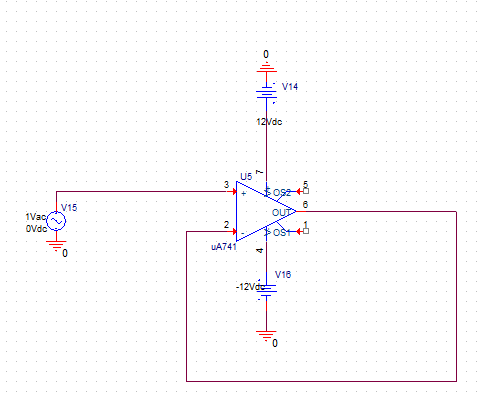
Para \( G_V = 100 \) el esquemático es el siguiente:

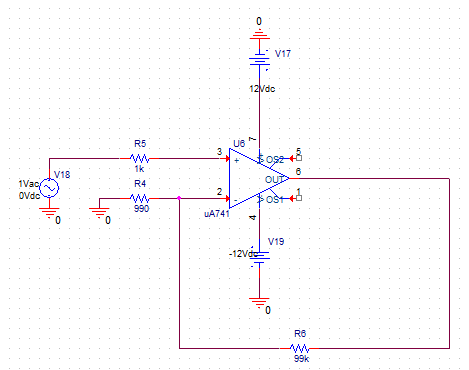
Para \(G_V = -100 \) el esquemático es el siguiente:

La gráfica es la siguiente donde el color verde es para \(G_V = 1 \), el color rojo para \(G_V = 100 \) y el azul para \(G_V = -100 \):

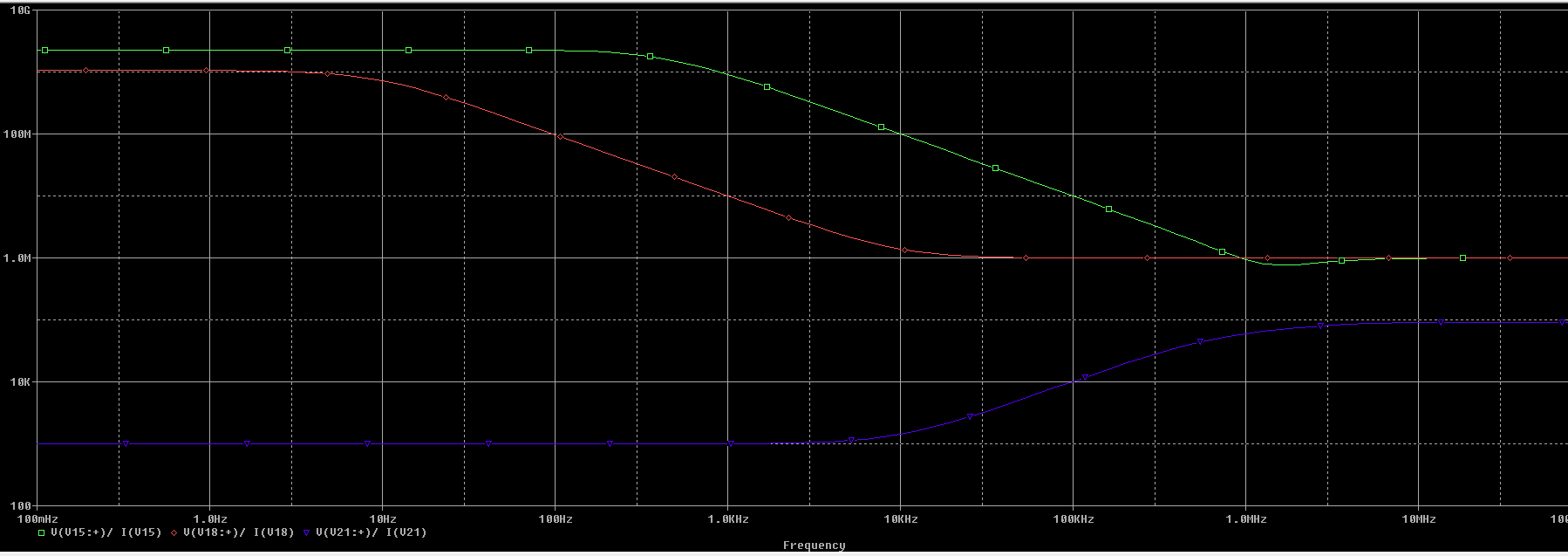
Los valores obtenidos son los siguientes: $$ Z_{iCR}(G_v = 1) = 2.28 \ G\Omega \\ Z_{iCR}(G_v = 100) = 1 \ G\Omega \\ Z_{iCR}(G_v = -100) = 1 \ K\Omega \\ $$

5.c -Impedancia de salida ZoCR(f): represente en una gráfica la evolución de ZoCR(f) para el amplificador seguidor (GV = 1) y compare con el valor esperado teóricamente.

El esquemático es el siguiente:

La gráfica para obtener \(Z_{oCR}(f)\) es la siguiente:

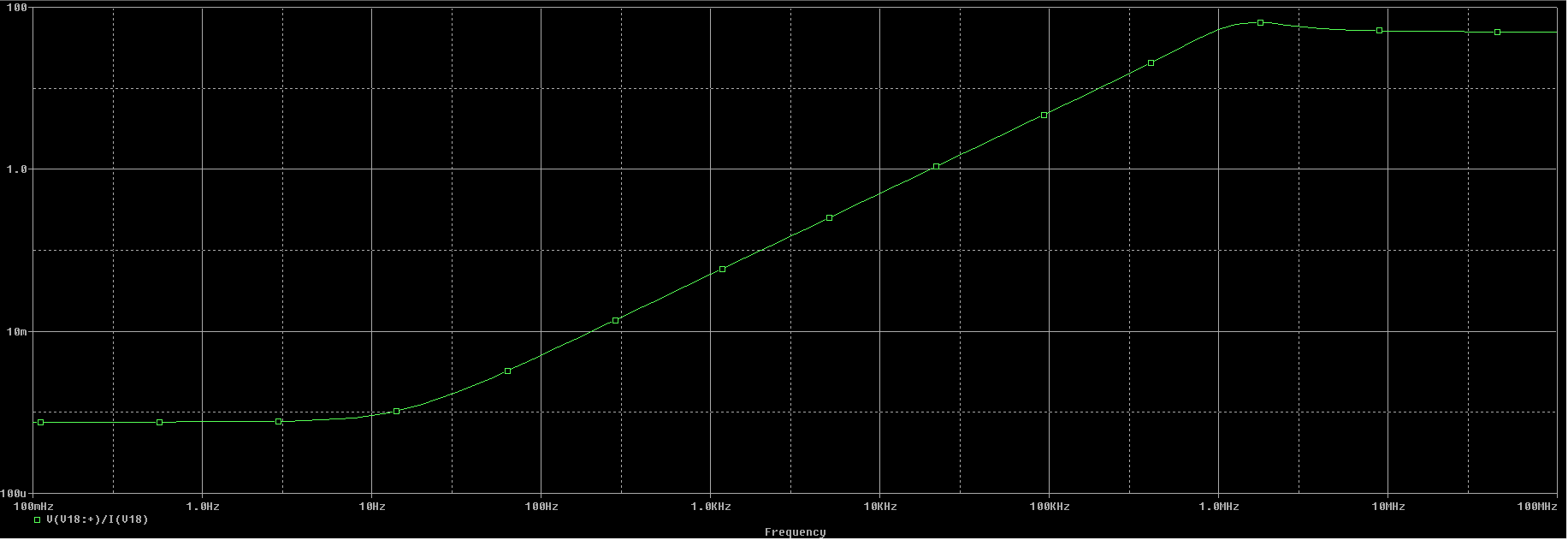
Observando la gráfica obtenemos que para baja frecuencia: $$ Z_{oCR} = 761.39 \ \mu \Omega $$

El valor esperado teóricamente es: $$ Z_{oCR} = \frac{R_0}{1 + A_{md} \cdot \beta} = \frac{151.7}{1 + 2 \cdot 10^5} = 758.49 \ \mu \Omega $$

Los dos valores son muy cercanos.

Ejercicio 6 - Oscilador

6.a -Obtenga los valores de los componentes necesarios y las características del tren de pulsos y de la señal de control Vm, para cumplir las siguientes especificaciones: Amplitud de 5 V, f = 100 kHz, THmin = 3 us (D = 0.3), THmax = 8 us (D = 0.8).

El montaje monoestable con el integrado 555 tiene el siguiente periodo.

$$ T = R \cdot C \cdot \ln{[\frac{V_{cc}}{V_{cc}-V_{TH}}]} = R \cdot C \cdot \ln{3} $$

Como nos dan la frecuencia en el enunciado, impondremos que \(R = 10 \ k\Omega\) y hallaremos C de la siguiente forma:

$$ \frac{1}{100 \ KHz} = 10000 \cdot \ C \cdot \ln{3} \Rightarrow C \approx 1 nF $$

El montaje de modulación PWM con el temporizador 555 seguirá que \( T_H = RC \ \ln{ [ \frac{V_{CC}}{V_{CC}-V_m} ] } \). Conociendo \(T_{Hmin}\), \(T_{Hmax}\) y \(V_{CC} = 5 \ V\) procederemos así:

$$ 8 \cdot 10^{-6} = 10000 \cdot 1 \cdot 10^{-9} \cdot \ln{(\frac{5}{5-V_{m_{max}}})} \Rightarrow V_{m_{max}} = 2,75 \ V \\ 3 \cdot 10^{-6} = 10000 \cdot 1 \cdot 10^{-9} \cdot \ln{(\frac{5}{5-V_{m_{max}}})} \Rightarrow V_{m_{max}} = 1,3 \ V $$

Con lo que podremos calcular los siguientes valores de la señal \(V_m\): $$ V_{offset} = \frac{V_{m_{max}} + V_{m_{min}}}{2} = 2.03 \ V \\ V_{ampl} = V_{m_{max}} - V_{offset} = 0.73 \ V $$

El tren de pulsos tendrá las siguientes características: $$ V_1 = 5 \ V \\ V_2 = 0 \ V \\ TD = 20 \ \mu s \\ TR = 2 \ ns \\ TF = 2 \ ns \\ PW = 3 \ \mu s \\ PER = 10 \ \mu s \\ $$

6.b -Simule en PSPICE el circuito diseñado (análisis transitorio) y justifique las diferencias con el resultado esperado. Para generar el tren de pulsos, utilice un generador de tensión tipo VPULSE, con los siguientes parámetros: DC (no necesario para análisis transitorio), AC (no necesario para análisis transitorio), V1= (nivel de tensión 1), V2= (nivel de tensión 2), TD= (tiempo de retardo del primer pulso desde t=0), TR= (tiempo de subida de V1 a V2), TF= (tiempo de bajada de V2 a V1)), PW= (anchura del pulso de valor V2), PER= (periodo de repetición del pulso).

Poniendo el tren de pulsos Vt2 y la señal de contrl Vc2 cómo hemos descrito anteriormente nos sale lo siguiente:

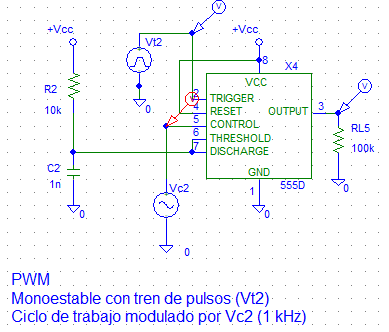
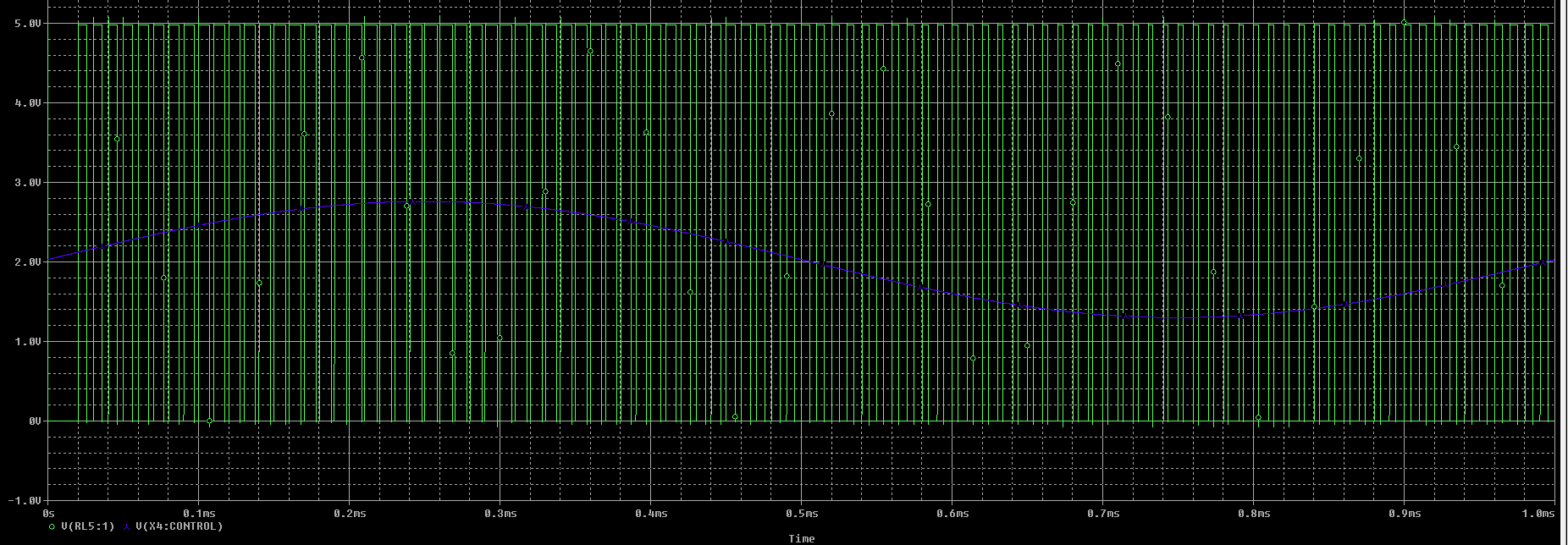
Midiendo los ciclos de trabajo en la simulación se puede ver cómo lo calculado en la teória se puede contrastar con la simulación. Cumpliendose que: $$ T_{H_{min}} = 3 \ \mu s \\ T_{H_{max}} = 8 \ \mu s $$

6.c- OPCIONAL: Diseñe con el 555D (montaje aestable), el generador del tren de pulsos necesario para el PWM del apartado 6.a. Simule en PSPICE el circuito completo (generador de pulsos + PWM).

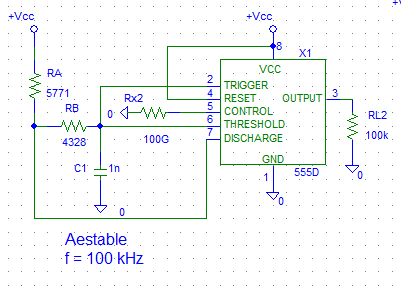
Con las ecuaciones del montaje aestable del 555 procedemos de la siguiente forma.: $$ C = 1 \ nF \\ T_L = 3 \cdot 10^{-6} = R_B \cdot C \cdot \ln{2} \Rightarrow R_B = 4328 \ \Omega \\ T_H = 7 \cdot 10^{-6} = (R_A + R_B) \cdot C \cdot \ln{2} \Rightarrow R_A = 5771 \Omega $$

El aestable tendrá el siguiente esquemático:

Y la simulación al completo del circuito del generador de pulsos + PWM tendrá la siguiente forma:

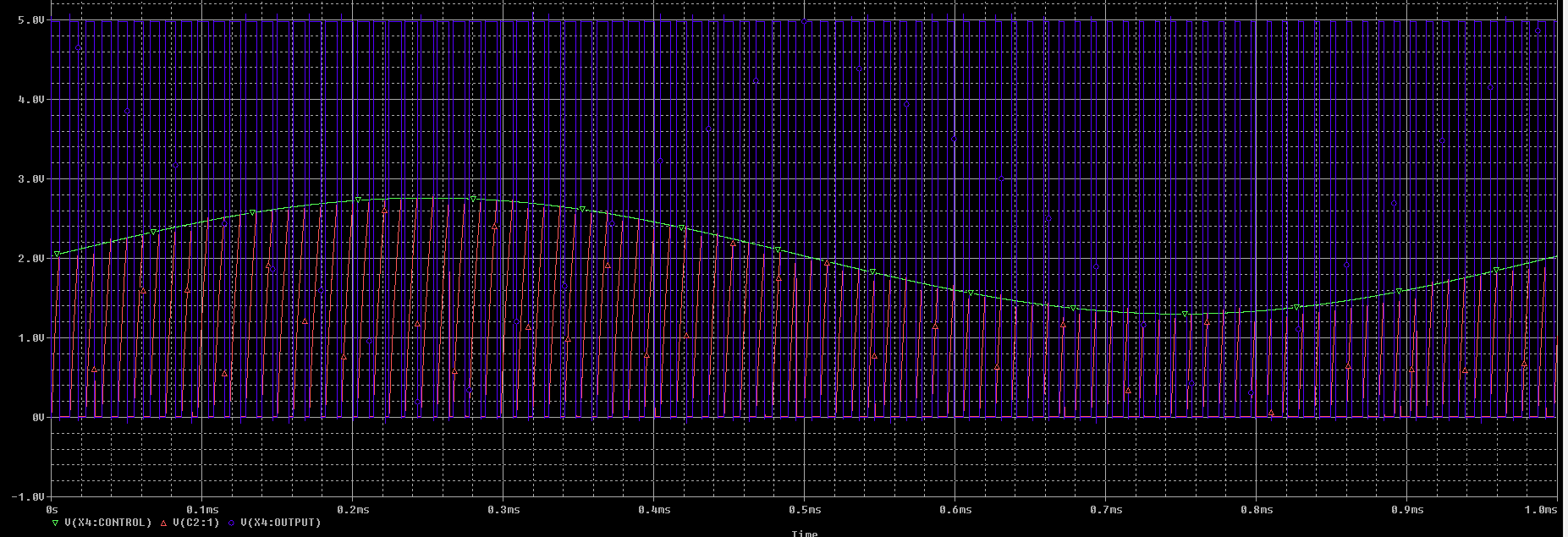
He podido ver que el aestable no es muy preciso, dando un error de \( +0.3 \ \mu s \). Entiendo que será un pequeño error en la simulación.