There a two elements that define an array, the element pattern and the array factor:

$$ E = E_{ref} \cdot AF $$ $$ AF = \sum_{n=1}^N e^{(n-1)\beta} e^{jk(n-1)d\cos{\theta}} \\ \psi = kd\cos{\theta} + \beta \\ AF_n = \frac{\sin(N\psi / 2)}{N \sin(\psi / 2)} $$ Where \(\beta\) is the progressice phase shift, N the number of elements, d the distance between elements, \(\theta\) the angle from the axis of the array to the observation point.

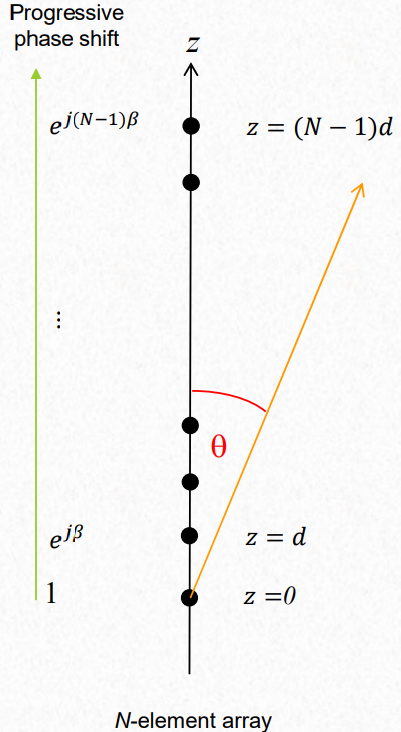
The maximum array factor is found when:

$$ \lvert AF_n \lvert = 1 \rightarrow \psi = 2 m \pi $$ I computed that in python because I was not sure, and it is exactly that xD:

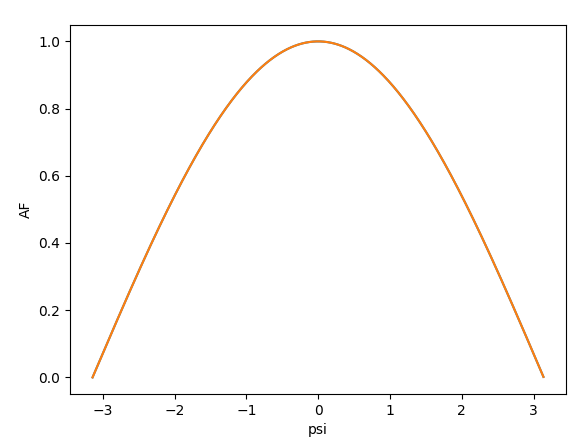
Uniform linear array

The grating lobes plot:

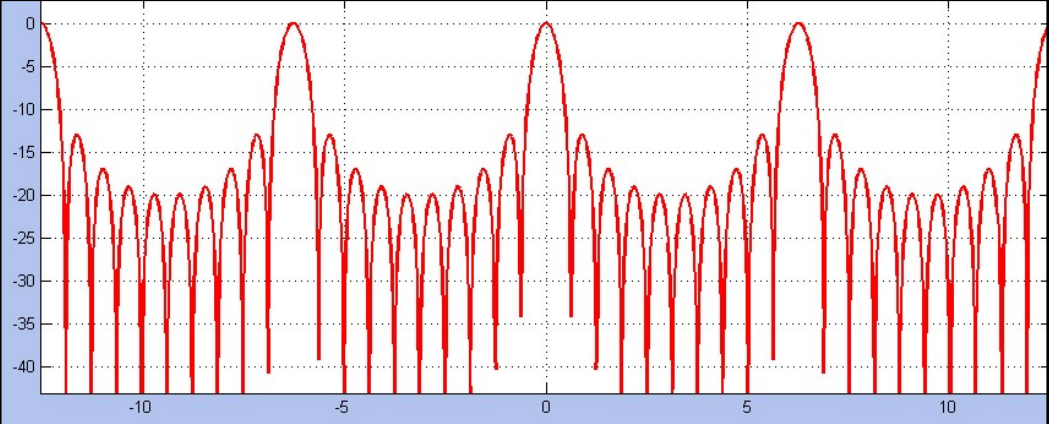
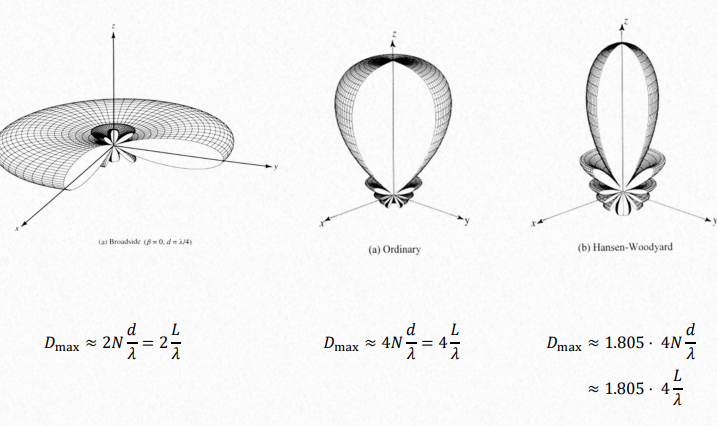
Broadside array

In broadside the maximum is in \(\theta = \pi / 2\).

$$ \theta = \pi / 2 \Rightarrow \psi = \beta \\ AF_n = max \Rightarrow \psi = 2 m \pi \\ \Rightarrow \beta = 2 m \pi \Rightarrow \beta = 0 \\ \Rightarrow AF_n = \frac{\sin(N k d \cos{\theta / 2})}{N \sin(k d \cos{\theta} / 2)} $$

Thus to have the maximum of the array factor of a uniform linear array directed broadside to the axis of the array, it is necessary that all the elements have the same phase excitation (in addition to the same amplitude excitation).

To avoid any grating lobe, the largest spacing between the elements should be less than one wavelength (dmax < λ).

Endfire array

In broadside the maximum is in \(\theta = 0\).

$$ \theta = 0 \Rightarrow \psi = kd + \beta \\ AF_n = max \Rightarrow \psi = 2 m \pi \\ \Rightarrow \beta = 2 m \pi - kd \Rightarrow \beta = -kd \\ \Rightarrow AF_n = \frac{\sin(N k d (\cos\theta - 1) / 2)}{N \sin(k d (\cos\theta - 1) / 2)} $$

To have only one end-fire maximum and to avoid any grating lobes, the maximum spacing between the elements should be less than dmax < λ/2.

Hansen-Woodyard endfire array

$$ \beta \approx -kd - \frac{\pi}{N} \\ d \approx \lambda / 4 $$

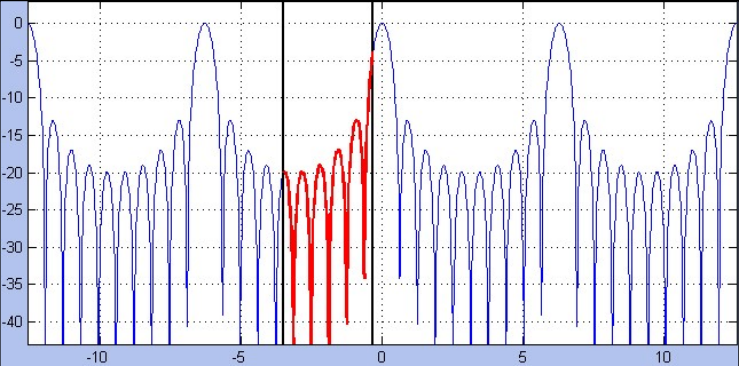
Non-uniform linear array

Even number of elements

For a even number of elements:

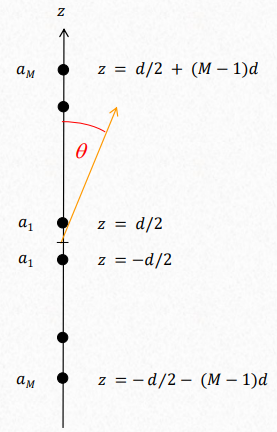
$$ AF_{2M} = \sum_{m=1}^{M} a_m \cos(\frac{2m -1}{2} kd \cos{\theta}) \\ max(AF_{2m}) = \sum_{m=1}^{M} a_m $$

Odd number of elements

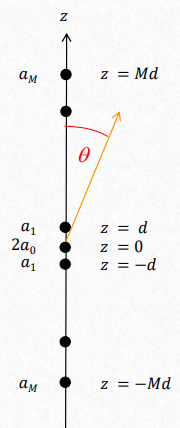
$$ AF_{2M+1} = 2a_0 \sum_{m=1}^{M} a_m \cos(m kd \cos{\theta}) \\ $$

Binomial array

Use the coefficients from pascal piramid. Some important values:

$$ HPBW \approx \frac{0.75}{\sqrt{L / \lambda}} \\ D_{max} \approx 1.77 \sqrt{N} = 1.77 \sqrt{1 + 2 L / \lambda} $$

Dolph-Tschebyscheff array

$$ T_m(\cos u) = \cos(m \ u) $$

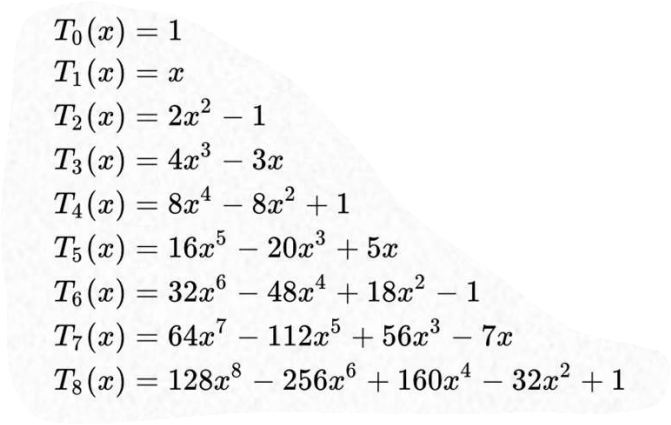
The indices are selected like in a filter.