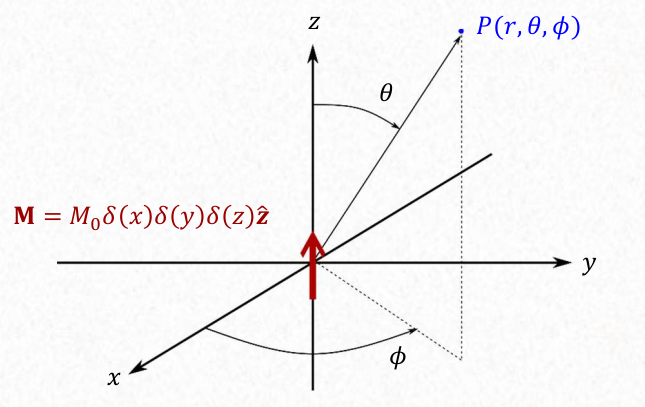
The properties of a magnetic dipole can be derived from those of the electric dipole. The magnetic dipole is called Fitzgerald dipole:

$$ [M] = [V \cdot m] \\ J \rightarrow \frac{M}{\eta_0} \quad \Rightarrow A_0 \rightarrow \frac{M_0}{\eta_0} \\ E \rightarrow \eta_0 H \Rightarrow H \rightarrow - \frac{E}{\eta_0} $$

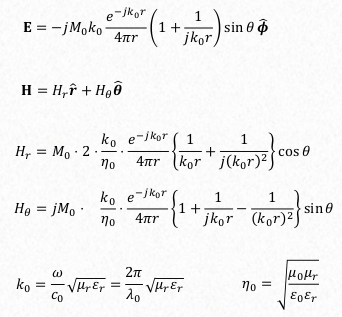
The complex Poynting vector due to a magnetic dipole is the conjugate complex of the complex Poynting vector of an electric dipole when radiating into a lossless medium. In the case of a lossy medium, an additional phase term appears but the magnitude remains the same:

$$ S_{FD} = S^*_{HD} $$ Similar to the Hertzian dipole we get the complex power:

$$ P = \bar P_{rad} + j Q = \frac{1}{\eta_0} \big ( \frac{\pi}{3} \big ) \big \lvert \frac{k_0 M_0}{2 \pi} \big \lvert^2 \big ( 1 + \frac{j}{(k_0 r)^3} \big ) \\ Q = + \frac{1}{\eta_0} \big ( \frac{\pi}{3} \big ) \big \lvert \frac{k_0 M_0}{2 \pi} \big \lvert^2 \frac{1}{(k_0 r)^3} $$

Follows, that 𝑄 > 0 and therefore that the stored magnetic energy \(W_m\) is larger than the stored electric energy \(W_e\). Thus, the Fitzgerald dipole has a inductive behaviour.

The normalized radiation intensity F, the directivity D and the effective area, are going to be the same as a hertzian dipole.

Small loop

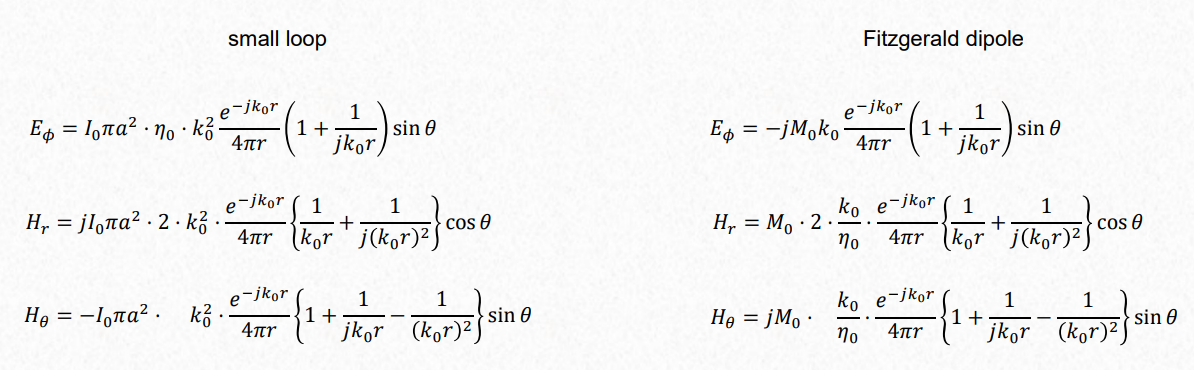
This satisfies when:

$$ M_0 = j I_0 \pi a^2 \eta_0 k_0 = j \omega \mu_0 I_0 \pi a^2 $$ Where a is the radious of the loop.

Because of the equivalence, we can apply the expressions for directivity, etc. of the Fitzgerald dipole also for the small loop.

Circular loop of constant current

This is valid for larger loop diameters. The expressions are for the Far field.

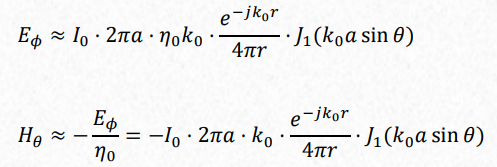
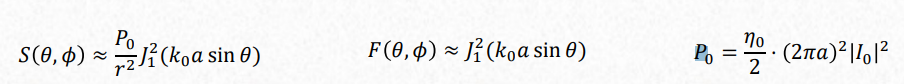
Where \(J_1\) is the 1st order Bessel function of the 1st kind.

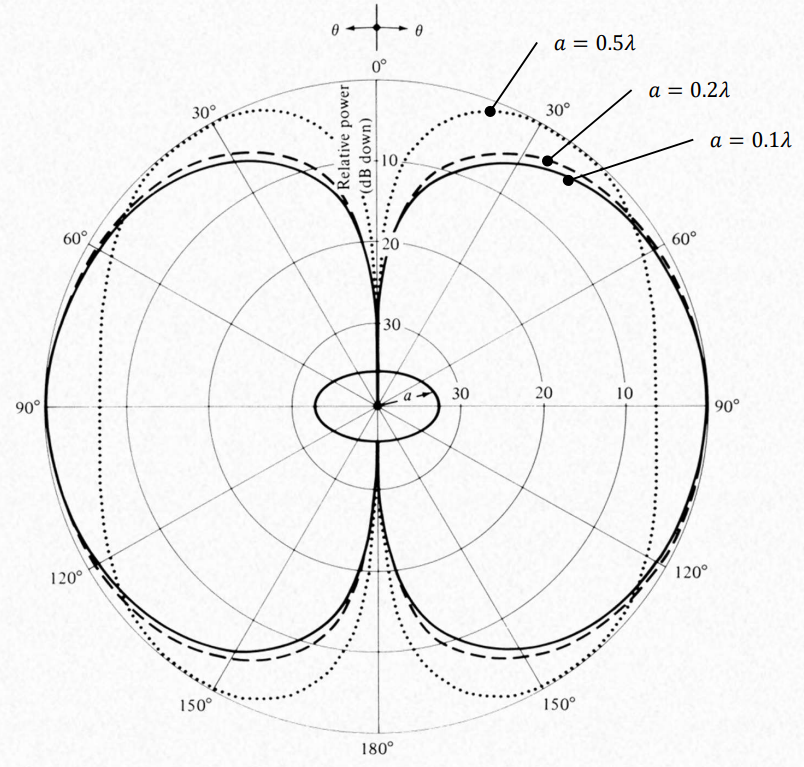
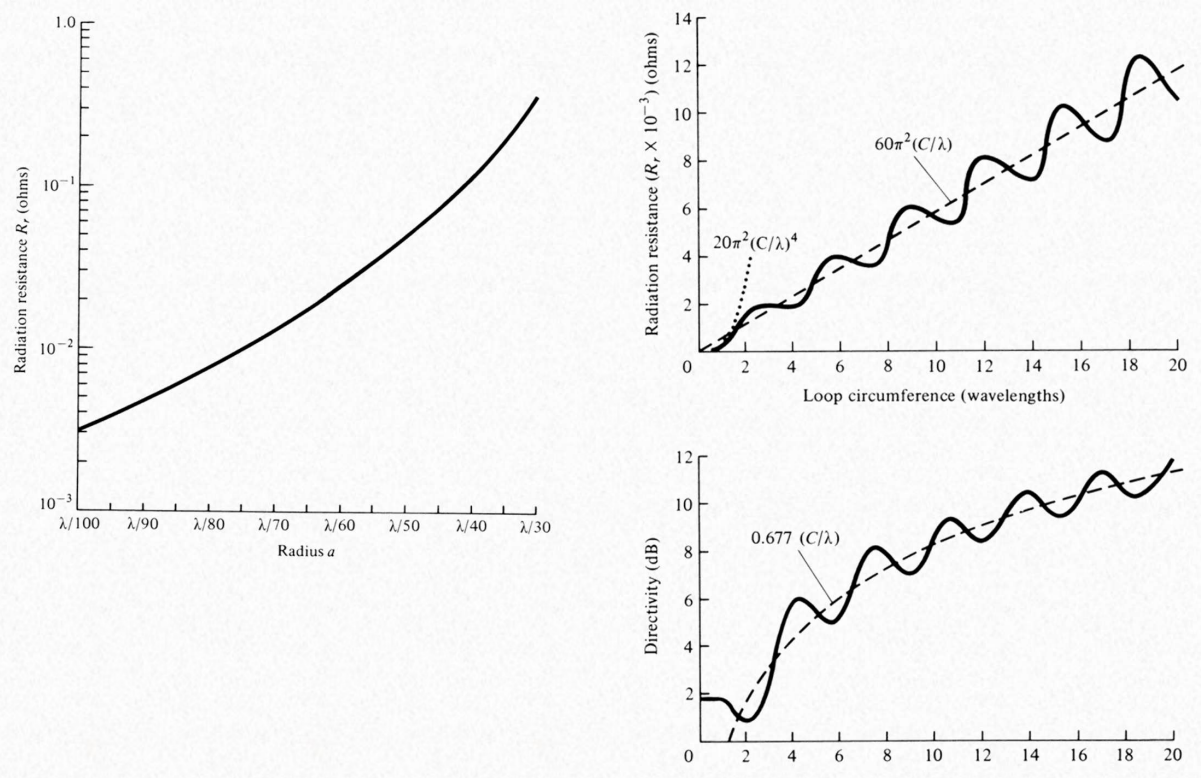
Beyond \(a > 0.61 \lambda\) the radiation along the loop’s plane (𝜃 = 90º) begins to intensify again and the pattern attains a multilobe form.

A loop antenna of Perimeter the wavelength is considered as fundamental as a half lambda dipole.