Generation sequences define the operations of the code. Basically it is a matrix defined this way:

$$ \text{Binary information} = u = (u_0, u_1, u_2, …) \\ \text{Generating sequences} \Rightarrow \\ g^{(0)} = (g^{(0)}_0, g^{(0)}_1, g^{(0)}_2, … g^{(0)}_M) \\ … \\ g^{(n-1)} = (g^{(n-1)}_0, g^{(n-1)}_1, g^{(n-1)}_2, … g^{(n-1)}_M) $$

The n convolutions produce n sequences: $$ v^{(0)}_j = g^{(0)}_0 u_j + g^{(0)}1 u{j-1} + … + g^{(0)}M u{j-M} \\ … \\ v^{(n-1)}_j = g^{(n-1)}_0 u_j + g^{(n-1)}1 u{j-1} + … + g^{(n-1)}M u{j-M} $$

The n sequences are multiplexed in a serial stream v:

$$ v = (v_0^{(0)}v_0^{(1)}, v_1^{(0)}v_1^{(1)}, v_2^{(0)}v_2^{(1)}, …. v_M^{(0)}v_M^{(1)}) $$

The memory (M) of the code is the generator length -1.

$$ R = \frac{1}{n} $$

A representation of an encoder. Pay attention that the bit is entering from \(u_{j-1}\ that is from the right.

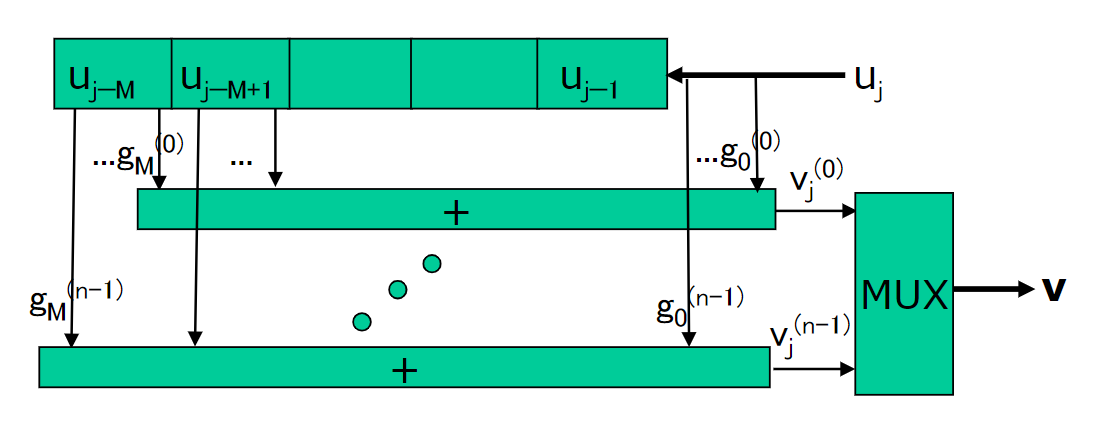So. the stattes are generated:

$$ \text{When next state is } u_j = 0 \Rightarrow u_{next} = (u_{j-M+1} … u_{j-1} \ 0) \\ \text{When next state is } u_j = 1 \Rightarrow u_{next} = (u_{j-M+1} … u_{j-1} \ 1) $$

V is generated as:

$$ v = (v_0 … v_{N-1}) = (u_0 … u_{K-1}) G’ = uG’ \\ \text{With noise} \Rightarrow v = [s u] G' $$

The generation matrix are generated the next way. In this example \(g^{0} = (111)\) and \(g^{1} = (101)\). Pay attention that the generation matrix consist in put g(0) vertically and then g(1).

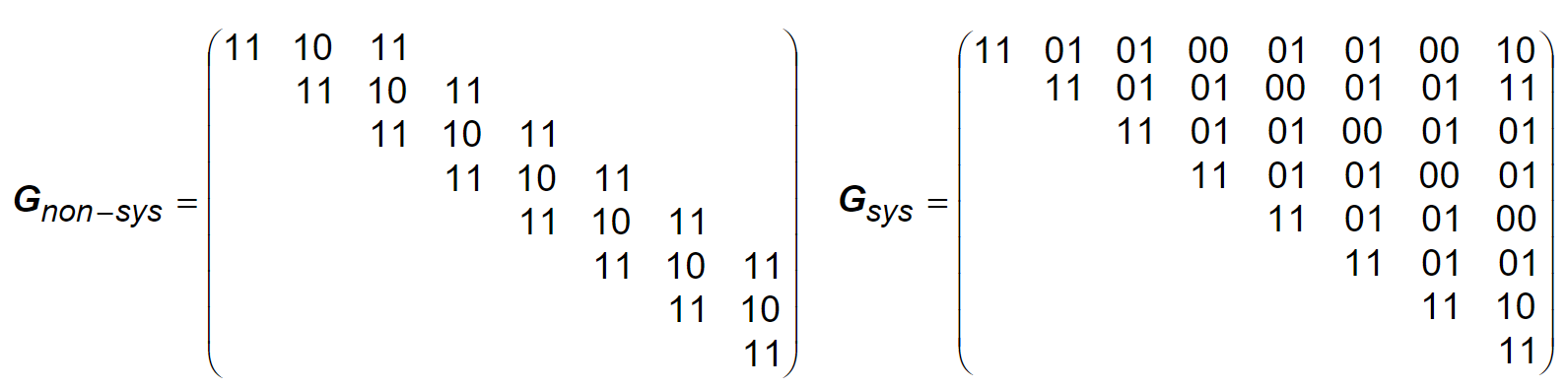
Dudas:

• No consigo entender systematic and non-systematic codes, cómo se genera la matriz generadora de las non sistematric.