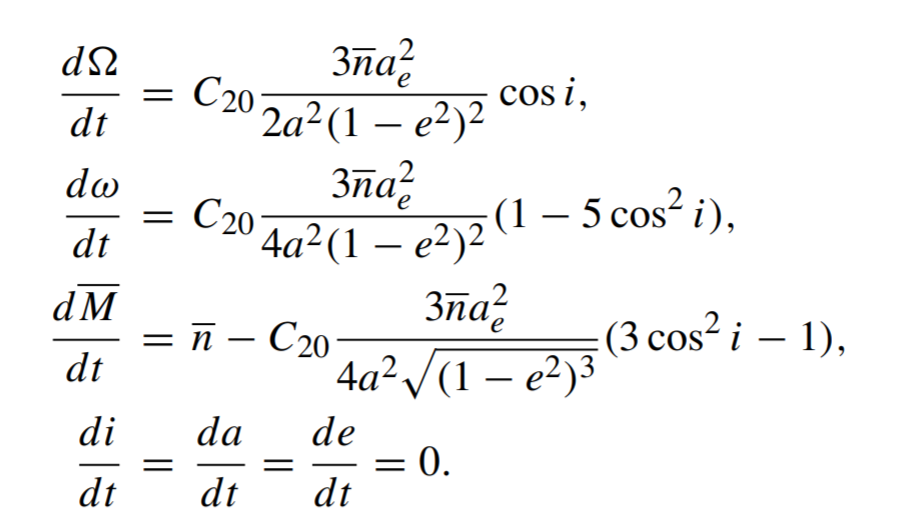Orbit pertubation forces
The general orbit of a satellite can be described using the Kepler elements as introduced earlier. The assumption in the Kepler description is that the central body (i.e. the Earth) can be described as a point mass and gravity from this body is the only force acting on the satellite.
This is of course far from the truth. Therefore, we are going to explore a more elaborated describtion where we include perturbations of the orbit and the evolution of the Kepler elements over time.
The non spherical Earth
First we look at the Earth gravity field formulated as spherical harmonic functions and investigate how it affects the the orbit. To simplify the investigation we only consider the pertubation from the second zonal part of the gravity field. In the investigation we use the GRS80 definitions by H. Moritz (2000) adobted by IUGG as the basic parameters describing our Earth.
import numpy as np
from dataclasses import dataclass
import math
@dataclass
class grs80: # "Geodetic Reference System 1980", Moritz, H. (2000).
a: float = 6378137.0 # Semi major axis
GM: float = 3986005.0e8 # Earth standard gravitional parameter [m^3/s^2]
J2: float = 108263.0e-8 # Dynamical form factor
Kepler elements for Galileo
In the following exercise we look at the effect on the nominal orbit of the Galileo satellite GSAT0104 (E20, nickname Sif) as described by EUSPA, European GNSS Service Center. The Kepler elements below is referenced to 21/11/2016 0:00:00 UTC.
@dataclass
class galileo: # GSAT0104 from EUSPA, European GNSS Service Center
a: float = 29599.8e3 # Semi-major axis [m]
e: float = 0.0 # Eccentricity
i: float = np.deg2rad(56.0) # Inclination [rad]
RAAN: float = np.deg2rad(197.632) # (Omega) Right ascension of the ascending node [rad]
omega: float = np.deg2rad(0) # Argument of Perigee [rad]
M: float = np.deg2rad(30.153) # Mean anomaly [rad]
Oblateness pertubations
The $J_2$ dynamical form factor describes the flattening or oblateness of the Earth and is equal to the negative second zonal coefficient $-C_{20}$ in the spherical harmonic expansion of the gravity field. $J_2$ is around 1000 times larger than the other spherical harmonics coefficients in the gravity fields and secular pertubations caused by $J_2$ is the single largest pertubation acting on a satellite in Earths vincinity.
Note: In geodesy it is common to use real coefficients instead of complex coefficients in the Legendre polynomials and the coefficients are often normalized, so be careful when calculating the spherical harmonic expansion.
J2 perturbation of the Kepler elements
Construct functions to calculate the perturbation of the six Kepler elements caused by $J_2$ after $dt$ seconds. Consider which parameters to give the functions besides $dt$.
EDIT: My explanation
n_mean = math.sqrt((grs80.GM) / (math.pow(galileo.a, 3)))
def da(dt,):
da = 0.0 # Your own function here
return da * dt
def de(dt,):
de = 0.0 # Your own function here
return de * dt
def di(dt,):
da = 0.0 # Your own function here
return da * dt
def dRAAN(dt,):
dRAAN = -grs80.J2 * ((3 * n_mean * math.pow(grs80.a,2))/(2 * math.pow(galileo.a, 2) * math.pow((1 - math.pow(galileo.e, 2)), 2)))*math.cos(galileo.i) # Your own function here
return dRAAN * dt
def domega(dt,):
domega = -grs80.J2 * ((3 * n_mean * math.pow(grs80.a,2))/(4 * math.pow(galileo.a, 2) * math.pow((1 - math.pow(galileo.e, 2)), 2)))*(1- (5 * math.pow(math.cos(galileo.i), 2)))
return domega * dt
def dM(dt,):
dM = n_mean + grs80.J2 * ((3 * n_mean * math.pow(grs80.a,2))/(4 * math.pow(galileo.a, 2) * math.sqrt(math.pow((1 - math.pow(galileo.e, 2)), 3))))*(3* math.pow(math.cos(galileo.i), 2) -1)
return dM * dt
Use the function to calculate the rate of change for the six Kepler elements as $m/s$, $s^{-1}$, and $deg/s$.
print('Rate of change for the six Kepler elements')
print(f'da/dt: {da(1.0,): .6e} m/s')
print(f'de/dt: {de(1.0,): .6e} 1/s')
print(f'di/dt: {np.rad2deg(di(1.0,)): .6e} deg/s')
print(f'dRAAN/dt: {np.rad2deg(dRAAN(1.0,)): .6e} deg/s')
print(f'domega/dt: {np.rad2deg(domega(1.0,)): .6e} deg/s')
print(f'dM/dt: {np.rad2deg(dM(1.0,)): .6e} deg/s')
Rate of change for the six Kepler elements
da/dt: 0.000000e+00 m/s
de/dt: 0.000000e+00 1/s
di/dt: 0.000000e+00 deg/s
dRAAN/dt: -2.995032e-07 deg/s
domega/dt: 1.509006e-07 deg/s
dM/dt: 7.103254e-03 deg/s
The ascending node
Find the orbit period of GSAT0104 and calculate the right ascension of the ascending node after one orbit, 1 day, 3 months (i.e. quater of a year) and half a year.
GM = 3986004.418e8 # m^3/s^2
T = ((2 * math.pi) / math.sqrt(GM)) * math.pow(galileo.a, 3/2) # Your own function here
sday = 24*3600 # s
smonth = 30 * sday # s
syear = 12 * smonth # s
print(f'Orbit period: {T: .3f} sec')
print(f'RAAN(1 orbit): {np.rad2deg(galileo.RAAN + dRAAN(T,)): .3f} deg')
print(f'RAAN(1 day): {np.rad2deg(galileo.RAAN + dRAAN(1*sday, )): .3f} deg')
print(f'RAAN(3 months): {np.rad2deg(galileo.RAAN + dRAAN(0.25*syear, )): .3f} deg')
print(f'RAAN(0.5 year): {np.rad2deg(galileo.RAAN + dRAAN(0.5*syear, )): .3f} deg')
Orbit period: 50680.880 sec
RAAN(1 orbit): 197.617 deg
RAAN(1 day): 197.606 deg
RAAN(3 months): 195.303 deg
RAAN(0.5 year): 192.974 deg
Sunsynchronous orbit
Sometimes it is desireable to have an orbit where the orbital plane is fixed with respect to the sun, e.g. to ensure sufficient power from the solar panels. Such an orbit is caled sunsynchronous and the right ascension of the ascending node must therefore change as the Earth moves around the sun. We can then use the $J_2$ perturbation the “drive” the right ascension of the ascending node around the Earth in order to make the orbit sunsynchronous.
Inclination of a sunsynchronous orbit
We want to design an sunsynchronous orbit for a satellite in a circular orbit with a semi major axis of 7500 km. If we only consider the $J_2$ pertubation which inclination should we then choose?
Hint: the Rate of the right ascension of the ascending node $\frac{d\Omega}{dt}$ should be $\frac{360^\circ}{year}$ for a sunsynchronous orbit.
def i_ssync(a_ssync, e_ssync):
dRAAN = (2* math.pi) / syear
n_mean = math.sqrt((grs80.GM) / (math.pow(a_ssync, 3)))
# Clear cos_i from the dRAAN equation
cos_i = 1/ (-grs80.J2 * ((3 * n_mean * math.pow(grs80.a,2))/(2 * dRAAN * math.pow(a_ssync, 2) * math.pow((1 - math.pow(e_ssync, 2)), 2)))) # Your own function here
i_ssync = math.acos(cos_i) # Get the angle
return i_ssync
a_ssync = 7500.0e3 # [m]
e_ssync = 0.0
print(f'Inclination of sunsyncronious orbit: {np.rad2deg(i_ssync(a_ssync, e_ssync)): .3f} deg')
Inclination of sunsyncronious orbit: 100.192 deg
Extreme sunsynchronous orbit
If you try to determine which inclination a Galileo satellite should have to be sun synchronous it fails because there is a limit to how large the orbit can be an still be sunsynchronous. Determine the maximum semi major axis $a$ and corresponding inclination $i$ for a circular ($e=0.0$) sunsynchronous orbit.
e_ssync = 0.0
a_ssync = 0.0 # Your own functions here
dRAAN = (2* math.pi) / syear
# Clear the assync from the dRAAN equation
a_ssync = math.pow(-grs80.J2 * ((3 * math.sqrt(grs80.GM) * math.pow(grs80.a,2))/(2 * dRAAN * math.pow((1 - math.pow(e_ssync, 2)), 2)))* -1, 2/7)
print('Extreme sunsyncronious orbit')
print(f'Semi major axis: {a_ssync: .3f} m')
print(f'Inclination: {np.rad2deg(i_ssync(a_ssync, e_ssync)): .3f} deg')
Extreme sunsyncronious orbit
Semi major axis: 12301589.423 m
Inclination: 180.000 deg