- Explicar las diferencias entre los controladores vistos en el aula (P, PD, P-D, PI, PID, PI-D, PID-D y D|PID) desde la perspectiva del seguimiento de señales de referencia monómicas y el comportamiento de régimen transitorio, explicando cómo afectan los parámetros \(K_P\), \(\tau_D\) y \(\tau_I\) a cada uno de ellos (20 %).
Utilizar como ejemplo a controlar la función de transferencia simplificada del motor DC:
$$ G(s) = \frac{K}{s \cdot (s+p)} $$
Controlador P
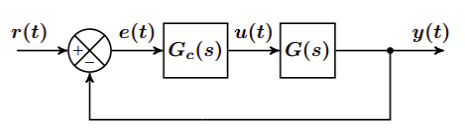
Donde la función de transferencia del sistema puede expresarse como:
$$ H(s) = \frac{G_C(s) \cdot G(s)}{1 + G_C(s) \cdot G(s)} $$
En el dominio de Laplace será \(G_c(s) = K_p\) y \(G(s) = \frac{K}{s \cdot (s+p)}\), por lo que la función de transferencia en lazo cerrado se podría dibujar de la siguiente forma:
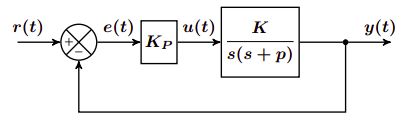La función de transferencia del lazo cerrado será:
$$ H_P(s) = \frac{K_p \cdot K}{s^2 + ps + K_p \cdot K} $$
De la expresión anterior se puede observar que el numerador contiene un “subpolinomio completo” del denominador de grado 0. Por lo que el error del sistema en regimen permanente será:
- \(e_{SS,0}(\infty) = 0 \Rightarrow\) para señales de entrada monómicas de orden 0, esto es, señales escalón.
- \(e_{SS,1} (\infty) = \frac{4 \cdot \xi^2}{p} \Rightarrow\) para señales monómicas de orden 1, señales de tipo rampa. El error disminuirá si disminuye el valor de \(\xi\).
- \(e_{SS,2}(\infty) = \infty \Rightarrow\) para señales de orden 2, señales de tipo parábola
El controlador P sólo se verá afectado por el parámetro \(K_p\), pues su F.T. depende de este valor. Se va a realizar un estudio de cómo afecta la variación de \(K_P)\ a la salida del controlador.
Al aumentar el valor de \(K_p\) aumentar el valor de los polos complejos del lazo cerrado, que hace que hayan más oscilaciones, y aumenta la sobreenloganción máxima \(M_p\). El tiempo de establecimiento \(t_s\) es el mismo en los distintos casos. Podemos concluir con lo siguiente:
$$ K_p \uparrow \quad \Rightarrow \begin{cases} oscilaciones \uparrow \\ M_p \uparrow \end{cases} $$
Controlador P-D
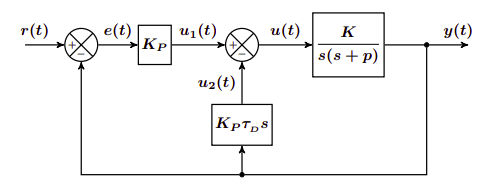
El controlador P-D consiste en un sistema de control realimentado con un controlador de tipo proporcional y derivativo con el factor proporcional en el lazo directo y el factor derivativo en el lazo paralelo. La F.T del controlador es la siguiente:
$$ H_{P-D}(s) = \frac{K_p \cdot K}{s^2 + s(p + K_p \cdot K \cdot \tau_D) + K_p \cdot K} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 0. Puesto que es de orden 0, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = 0 \Rightarrow\) Para señales de referencia de tipo escalón.
- \(e_{SS,1} (\infty) = \frac{2 \cdot \beta_2\xi^2}{p} \Rightarrow\) Para señales de referencia tipo rampa. En este caso, para reducir el error deberán reducirse los parámetros \(\beta_2\) y \(\xi\).
- \(e_{SS,2}(\infty) = \infty \Rightarrow\) Para señales de referencia tipo parábola.
El controlador P sólo se verá afectado por los parámetros \(K_p\) y \(\tau_D\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En primer lugar veremos la respuesta del controlador con la variación del valor de \(K_p\) manteniendo constante el valor de \(\tau_d\). Cuando aumenta el valor de \(K_p\) hace que aumente el tiempo de establecimiento \(t_s\), y la sobreenlonganción máxima \(M_p\) no se ve muy afectada.
$$ K_p \uparrow \quad \Rightarrow \begin{cases} oscilaciones \uparrow \\ t_s \uparrow\end{cases} $$
En segundo lugar, veremos la respuesta del controlador con la variación del valor \(\tau_d\) manteniendo constante \(K_p\). Aumentando el valor de \(\tau_d\) hacemos que aumente la estabilidad del sistema, reduciendo el número de oscilaciones y el tiempo de establecimiento \(t_s\). El valor de la sobreenlonganción máxima \(M_p\) no se ve muy afectada.
$$ \tau_d \uparrow \quad \Rightarrow \begin{cases} oscilaciones \downarrow \\ t_s \downarrow\end{cases} $$
El comportamiento derivatico del controlador hace que se comporte de la siguiente forma:
$$ y(t=0) = 0 $$
Esto implica que la curva empieza tangente al eje t, teniendo un arranque suave.
Controlador PD
Este controlador tiene el siguiente esquema:
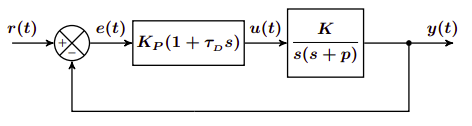
La función de transferencia de este controlador es la siguiente:
$$ H_{PD}(s) = \frac{K_p \cdot K (1 + \tau_D \cdot s)}{s^2 + s(p + K_p \cdot K \cdot \tau_D) + K_p \cdot K} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 0. Puesto que es de orden 0, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = 0 \Rightarrow\) Para señales de referencia de tipo escalón.
- \(e_{SS,1} (\infty) = \frac{2 \cdot \beta_2\xi^2}{p} \Rightarrow\) Para señales de referencia tipo rampa. En este caso, para reducir el error deberán reducirse los parámetros \(\beta_2\) y \(\xi\)
- \(e_{SS,2}(\infty) = \infty \Rightarrow\) Para señales de referencia tipo parábola.
El controlador PD sólo se verá afectado por los parámetros \(K_p\) y \(\tau_D\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En primer lugar veremos la respuesta del controlador con la variación del valor de \(K_p\) manteniendo constante el valor de \(\tau_d\). Cuando aumenta el valor de \(K_p\) hace que el sistema se vuelva más inestable y aumente ligeramente el tiempo de establecimiento \(t_s\), y la sobreenlonganción máxima \(M_p\) aumenta ligeramente.
$$ K_p \uparrow \quad \Rightarrow \begin{cases} M_p \uparrow \\ oscilaciones \uparrow \\ t_s \uparrow \end{cases} $$
En segundo lugar, veremos la respuesta del controlador con la variación del valor \(\tau_d\) manteniendo constante \(K_p\). Aumentando el valor de \(\tau_d\) hacemos que aumente la estabilidad del sistema, reduciendo el tiempo de establecimiento \(t_s\). El valor de la sobreenlonganción máxima \(M_p\) no se ve muy afectada. Para valores bajos de \(\tau_d\) aparecen polos complejos en lazo cerrado que aumentan las oscilaciones del sistema, con lo que aumentando dicho valor disminuirán las oscilaciones.
$$ \tau_d \uparrow \quad \Rightarrow \begin{cases} oscilaciones \downarrow \\ t_s \downarrow\end{cases} $$
La respuesta del controlador PD en el origen tiene el siguiente valor:
$$ y(t=0) = - \omega_n \cdot \xi \cdot (\beta_2 - 2) $$
La expresión anterior depende del valor de la constante \(\beta_2\), por lo que tendremos los siguientes escenarios:
- Si \(\beta_2 < 2\) hace que \(y(t=0) > 0\) lo que implica que el sistema tenga un arranque rápido.
- Si \(\beta_2 > 2\) hace que \(y(t=0) < 0\) lo que implica que el sistema arranca en sentido negativo.
- Si \(\beta_2 = 2\) hace que \(y(t=0) = 0\) lo que implica que el sistema tenga un arranque lento.
Controlador PI
El controlador PI tiene el siguiente esquema:
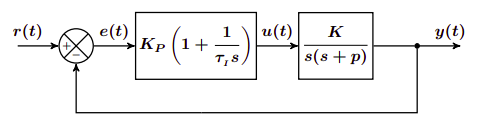
La función de transferencia en lazo cerrado del sistema puede escribirse de la siguiente forma:
$$ H_{PI}(s) = \frac{K_p \cdot K (s + \frac{1}{\tau_i})}{s^2(s+p) + K_p \cdot K (s + \frac{1}{\tau_i})} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 1. Puesto que es de orden 1, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = (e_{SS,1} (\infty) = 0 \Rightarrow\) Para señales de referencia monómicas hasta de orden 1: escalón y rampa.
- \(e_{SS,2} (\infty) = \frac{\tau_i \cdot p}{K_p \cdot K} = \frac{\beta_2^3 \cdot \xi^2}{p^2(\beta_2 - 2)} \Rightarrow\) Para señales de referencia tipo parábola. En este caso, para reducir el error deberán reducirse los parámetros \(\tau_i\), o bien aumentar \(\K_p\)
El controlador PI sólo se verá afectado por los parámetros \(K_p\) y \(\tau_i\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En primer lugar veremos la respuesta del controlador con la variación del valor de \(K_p\) manteniendo constante el valor de \(\tau_i\). Cuando aumenta el valor de \(K_p\) hace que el sistema se vuelva más inestable, aumentando las oscilaciones, el tiempo de establecimiento \(t_s\), y la sobreenlonganción máxima \(M_p\).
$$ K_p \uparrow \quad \Rightarrow \begin{cases} M_p \uparrow \\ oscilaciones \uparrow \\ t_s \uparrow \end{cases} $$
En segundo lugar, veremos la respuesta del controlador con la variación del valor \(\tau_i\) manteniendo constante \(K_p\). Aumentando el valor de \(\tau_i\) hacemos que aumente la estabilidad del sistema, reduciendo el tiempo de establecimiento \(t_s\). El valor de la sobreenlonganción máxima \(M_p\) disminuirá.
$$ \tau_i \uparrow \quad \Rightarrow \begin{cases} M_p \downarrow \\ oscilaciones \downarrow \\ t_s \downarrow\end{cases} $$
Controlador PID
El controlador PID tiene el siguiente esquema:
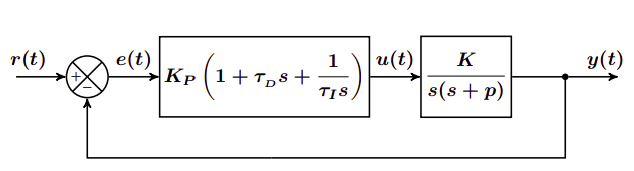
La función de transferencia del controlador será la siguiente:
$$ H_{PID}(s) = \frac{K \cdot K_p \cdot \tau_D (s^2 + \frac{s}{\tau_D} + \frac{1}{\tau_D \cdot \tau_i})}{s^2(s+p) + K \cdot K_p \cdot \tau_D (s^2 + \frac{s}{\tau_D} + \frac{1}{\tau_D \cdot \tau_i})} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 1. Puesto que es de orden 1, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = (e_{SS,1} (\infty) = 0 \Rightarrow\) Para señales de referencia monómicas hasta de orden 1: escalón y rampa.
- \(e_{SS,2} (\infty) = \frac{\beta_2^3 \cdot \xi^2}{\beta \cdot p^2} \Rightarrow\) Para señales de referencia tipo parábola. En este caso, para reducir el error deberán de disminuir el coeficiente de amortiguamiento \(\xi\) y la constante \(\beta_2\), o bien aumentar la constante \(\beta\).
El controlador PID sólo se verá afectado por los parámetros \(K_p\), \(\tau_d\) y \(\tau_i\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En este controlador existen polos con parte compleja lo que hará que haya oscilaciones. Al aumentar el valor de \(K_p\), \(\tau_d\) o \(\tau_i\) se da lugar a mayor estabilidad en el sistema y se reduce el tiempo de establecimiento \(t_s\) y la sobreenlonganción máxima \(M_p\).
$$ K_p \uparrow \quad \Rightarrow \begin{cases} M_p \downarrow \\ oscilaciones \downarrow \\ t_s \downarrow \end{cases} $$
Controlador PI-D
El controlador PI-D tiene el siguiente esquema:
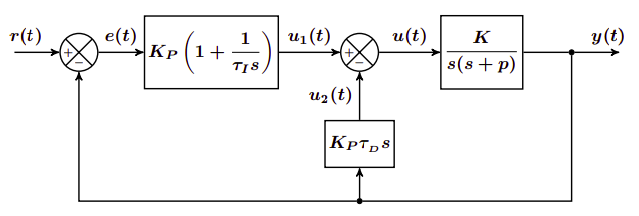
La función de transferencia del sistema es la siguiente:
$$ H_{PI-D}(s) = \frac{K \cdot K_p (s + \frac{1}{\tau_i})}{s^2(s+p) + K \cdot K_p \cdot \tau_D (s^2 + \frac{s}{\tau_D} + \frac{1}{\tau_D \cdot \tau_i})} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 1. Puesto que es de orden 1, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = (e_{SS,1} (\infty) = 0 \Rightarrow\) Para señales de referencia monómicas hasta de orden 1: escalón y rampa.
- \(e_{SS,2} (\infty) = \frac{\beta_2^2 \cdot (\beta + 2) \cdot \xi^2}{\beta \cdot p^2} \Rightarrow\) Para señales de referencia tipo parábola. En este caso, para reducir el error deberán de disminuir el coeficiente de amortiguamiento \(\xi\) y la constante \(\beta_2\).
El controlador PI-D sólo se verá afectado por los parámetros \(K_p\), \(\tau_d\) y \(\tau_i\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En este controlador existen polos con parte compleja lo que hará que haya oscilaciones. Un aumento en el valor de \(K_p\), \(\tau_d\) o \(\tau_i\) dará lugar a mayor estabilidad en el sistema y se reduce el tiempo de establecimiento \(t_s\) y la sobreenlonganción máxima \(M_p\).
$$ K_p \uparrow \quad \Rightarrow \begin{cases} M_p \downarrow \\ oscilaciones \downarrow \\ t_s \downarrow \end{cases} $$
Controlador PID-D
El controlador PID-D tiene el siguiente esquema
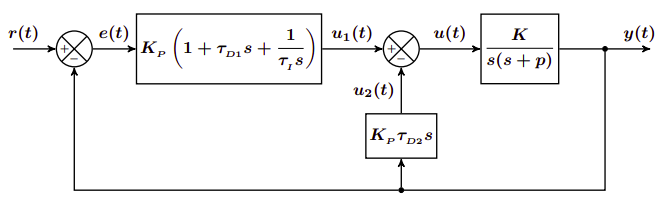
La función de transferencia del controlador es la siguiente:
$$ H_{PID-D}(s) = \frac{K \cdot K_p \cdot \tau_{D1} (s^2 + \frac{s}{\tau_{D1}} + \frac{1}{\tau_{D1} \cdot \tau_i})}{s^2(s+p) + K \cdot K_p \cdot \tilde \tau_D (s^2 + \frac{s}{\tilde \tau_D} + \frac{1}{\tilde \tau_D \cdot \tau_i})} \\ \tilde \tau_D = \tau_{D1} + \tau_{D2} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 1. Puesto que es de orden 1, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = (e_{SS,1} (\infty) = 0 \Rightarrow\) Para señales de referencia monómicas hasta de orden 1: escalón y rampa.
- \(e_{SS,2} (\infty) = cte \Rightarrow\) Para señales de referencia tipo parábola. En este caso, el error será nulo si \(K_p \tau_{D2} = - \frac{p}{K}\)
El controlador PID-D sólo se verá afectado por los parámetros \(K_p\), \(\tau_{d1}\), \(\tau_{d2}\) y \(\tau_i\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En este controlador existen polos con parte compleja lo que hará que haya oscilaciones. Una disminución en el valor de \(K_p\), \(\tau_{d1}\) o \(\tau_i\) dará lugar a menor estabilidad en el sistema, en el que aumentarán las oscilaciones y se aumenta el tiempo de establecimiento \(t_s\) y la sobreenlonganción máxima \(M_p\).
$$ K_p \uparrow \quad \Rightarrow \begin{cases} M_p \downarrow \\ oscilaciones \downarrow \\ t_s \downarrow \end{cases} $$
Por otra parte, un aumento del valor de \(\tau_D2\) hará que el sistema se vuelva más inestable, aumentando la sobreenlongación máxima \(M_p\), las oscilaciones y el tiempo de establecimiento \(t_s\).
$$ \tau_{d2} \uparrow \quad \Rightarrow \begin{cases} M_p \uparrow \\ oscilaciones \uparrow \\ t_s \uparrow \end{cases} $$
Controlador D|PID
El controlador D|PID tiene el siguiente esquema:
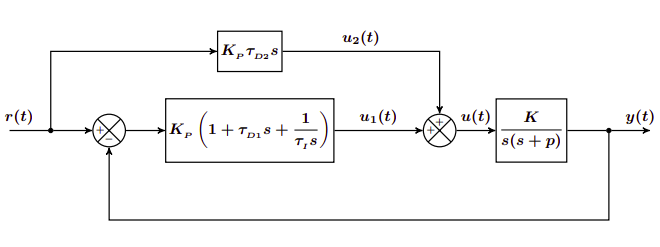
La función de transferencia de este controlador es la siguiente:
$$ H_{D|PID}(s) = \frac{K \cdot K_p \cdot \tilde \tau_{D} (s^2 + \frac{s}{\tilde \tau_{D}} + \frac{1}{\tilde \tau_{D} \cdot \tau_i})}{s^2(s+p) + K \cdot K_p \cdot \tilde \tau_{D1} (s^2 + \frac{s}{\tilde \tau_{D1}} + \frac{1}{\tilde \tau_{D1} \cdot \tau_i})} \\ \tilde \tau_D = \tau_{D1} + \tau_{D2} $$
El numerador contiene el “subpolinomio completo” del denominador de grado 1. Puesto que es de orden 1, el error en régimen permanente será:
- \(e_{SS,0}(\infty) = (e_{SS,1} (\infty) = 0 \Rightarrow\) Para señales de referencia monómicas hasta de orden 1: escalón y rampa.
- \(e_{SS,2} (\infty) = cte \Rightarrow\) Para señales de referencia tipo parábola. En este caso, el error será nulo si \(K_p \tau_{D2} = \frac{p}{K}\)
El controlador PID-D sólo se verá afectado por los parámetros \(K_p\), \(\tau_{d1}\), \(\tau_{d2}\) y \(\tau_i\). Se va a realizar un estudio de cómo afecta la variación de los diferentes parámetros a la respuesta del controlador.
En este controlador existen polos con parte compleja lo que hará que haya oscilaciones. Una disminución en el valor de \(K_p\), \(\tau_{d1}\) o \(\tau_i\), o un aumento del valor de \(\tau_{d2}\) dará lugar a menor estabilidad en el sistema, en el que aumentarán las oscilaciones y se aumenta el tiempo de establecimiento \(t_s\) y la sobreenlonganción máxima \(M_p\).
$$ K_p \uparrow \quad \Rightarrow \begin{cases} M_p \downarrow \\ oscilaciones \downarrow \\ t_s \downarrow \end{cases} \qquad \tau_{d2} \uparrow \quad \Rightarrow \begin{cases} M_p \uparrow \\ oscilaciones \uparrow \\ t_s \uparrow \end{cases} $$
Comparación de los resultados
| Controlador | \(e_{SS,0}(\infty)\) | \(e_{SS_1}(\infty)\) | \(e_{SS,2}(\infty)\) |
|---|---|---|---|
| P | 0 | \(cte = \frac{4 \xi^2}{p}\) | \(\infty\) |
| PD | 0 | \(cte = \frac{\beta_2^2 \xi^2}{p}\) | \(\infty\) |
| P-D | 0 | \(cte = \frac{2 \beta_2 \xi^2}{p}\) | \(\infty\) |
| PI | 0 | 0 | \(cte = \frac{2 \tau_i p}{K K_p}\) |
| PID | 0 | 0 | \(cte = \frac{\beta_2^3 \xi^2}{\beta p^2}\) |
| PI-D | 0 | 0 | \(cte = \frac{\beta_2^2 (\beta + 2) \xi^2}{\beta p^2}\) |
| PID-D | 0 | 0 | 0 si \(K_p \tau_{D2} = - \frac{p}{K}\) |
| D I PID | 0 | 0 | 0 si \(K_p \tau_{D2} = \frac{p}{K}\) |
| Controlador | \(\uparrow K_p\) | \(\uparrow \tau_d / \tau_{d1}\) | \(\uparrow \tau_{d2}\) | \(\tau_{i}\) |
|---|---|---|---|---|
| P | \(\uparrow oscilaciones, \quad \uparrow M_p\) | |||
| P-D | \(\uparrow osc, \quad \uparrow t_s\) | \(\downarrow osc, \quad \downarrow t_s\) | ||
| PD | \(\uparrow osc, \quad \uparrow M_p, \quad \uparrow t_s\) | \(\downarrow osc, \quad \downarrow t_s\) | ||
| PI | \(\uparrow osc, \quad \uparrow M_p, \quad \uparrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | ||
| PID | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | |
| PI-D | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | |
| PID-D | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\uparrow osc, \quad \uparrow M_p, \quad \uparrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) |
| D I PID | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) | \(\uparrow osc, \quad \uparrow M_p, \quad \uparrow t_s\) | \(\downarrow osc, \quad \downarrow M_p, \quad \downarrow t_s\) |
Notas Varias
- El script de matlab se basa en el dado en simulabo este