1. Modelar analíticamente el Motor-DC del TeleLabo.
a) Obtener la función de transferencia del motor utilizando las hojas de características del fabricante que se proporcionan en la web de la asignatura (A-max 32 - 30 V) (75 %).
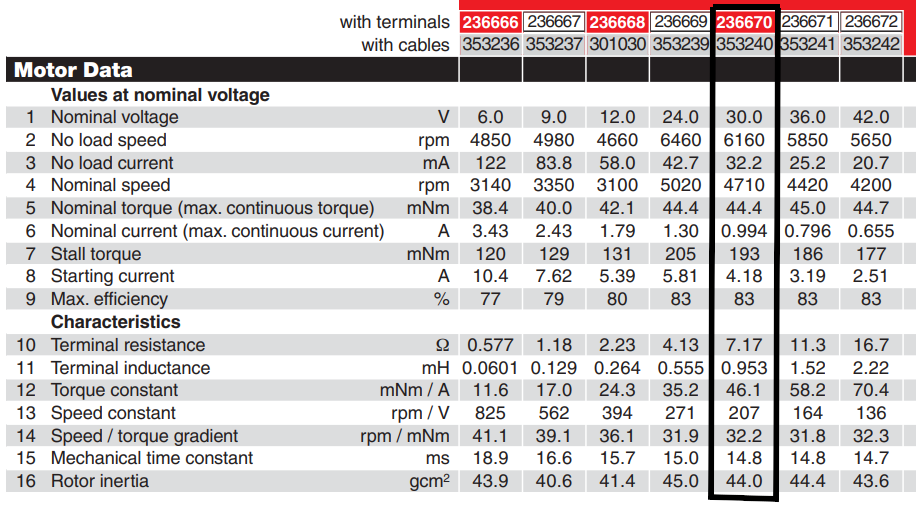
La hoja de características del motor se encuentra en este link.
En el enunciado nos indican que la tensión nominal del motor es de 30 V. Los valores asociados a esta tensión son los que se encuentra remarcados.
Convirtiendo los valores de la hoja de características al SI tendremos que:
| Parámetro | Valor | Unidad |
|---|---|---|
| \(U_N\) | \(30\) | \(V\) |
| \(R_m\) | \(7.17\) | \(\Omega\) |
| \(L_m\) | \(9.53 \cdot 10^{-4}\) | \(H\) |
| \(J_m\) | \(4.4 \cdot 10^{-6}\) | \(Kg \cdot m^2\) |
| \(t_m\) | \(1.48 \cdot 10^{-2}\) | \(s\) |
| \(t_e\) | \(1.33 \cdot 10^{-4}\) | \(s\) |
| \(k_b\) | \(4.61 \cdot 10^{-2}\) | \(V \cdot s / rad\) |
| \(k_m\) | \(4.61 \cdot 10^{-2}\) | \(N \cdot m / A\) |
| \(I_0\) | \(0.0322\) | \(A\) |
| \(\dot{\theta}_{mN}\) | \(645\) | \(rad/s\) |
Para calcular la constante de tiempo eléctrica \(t_e\) se hace de la siguiente forma:
$$ t_e = \frac{L_m}{R_m} = \frac{9.53 \cdot 10^{-4}}{7.17} = 1.33 \cdot 10^{-4} \ s $$
Con los datos anteriores podemos calcular el coeficiente de fricción viscosa. Se puede calcular utilizando dos métidos distintos:
- Utilizando la ecuación de la constante de tiempo mecánica, \(t_m\): $$ B_m = \frac{J_m}{t_m} - \frac{k_b \ k_m}{R_m} = \frac{4.4 \cdot 10^{-6}}{1.48 \cdot 10^{-2}} - \frac{4.61 \cdot 10^{-2} \cdot 4.61 \cdot 10^{-2}}{7.17} = 8.94 \cdot 10^{-7} $$
- Utilizando la ecuación de la corriente del motor sin carga, \(I_0\): $$ B_m = \frac{k_m \ I_0}{\dot{\theta}_{mN}} = \frac{4.61 \cdot 10^{-2} \cdot 0.0322}{645} = 2.3 \cdot 10^{-6} $$
Con el cálculo anterior hemos obtenido dos resultados disintos. Para obtener la función de transferencia más adecuada podemos hacer:
- Utiliza la media aritmética de los dos valores distintos de \(B_m\)
- Utiliza el valor más crítico para nuestro motor de \(B_m\)
- Hacer todos los calculos con los dos valores y comparar los resultados.
En esta práctica se va a optar por usar la opción 3 y comparar los resultados obtenidos.
Podremos calcular los polos de nuestra función de transferencia de la siguiente forma:
$$ p_{1,2} = - \frac{1}{2} \big ( \frac{1}{t_e} + \frac{1}{t’{m}} \big) \pm \frac{1}{2} \sqrt{ \big ( \frac{1}{t_e} - \frac{1}{t’{m}} \big)^2 - 4 \frac{k_m \ k_b}{J_m \ L_m} } \\ \text{donde} \qquad t’_{m} = \frac{J_m}{B_m} $$
Para \(B_m = 8.94 \cdot 10^{-7}\) obtendremos:
$$ t’_{m1} = \frac{4.4 \cdot 10^{-6}}{8.94 \cdot 10^{-7}} = 4.92 \\ p_1 = -68.23\\ p_2 = -7.45 \cdot 10^{3} $$
Para \(B_m = 2.3 \cdot 10^{-6}\) obtendremos lo siguiente:
$$ t’_{m2} = \frac{4.4 \cdot 10^{-6}}{2.3 \cdot 10^{-6}} = 1.913 \\ p_1 = -68.56 \\ p_2 = -7.45 \cdot 10^{3} $$
Con todos estos datos ya podremos calcular la función de transferencia utilizando la siguiente formula:
$$ G_{\dot{\theta_{m}}}(s) = \frac{K’_{m}}{(s - p_1) (s - p_2)} \\ \text{donde} \quad K’_m = \frac{k_m}{J_m \ L_m} = \frac{4.61 \cdot 10^{-2}}{4.4 \cdot 10^{-6} \cdot 9.53 \cdot 10^{-4}} = 10.994 \cdot 10^{6} $$
La función de transferencia para \(B_m = 8.94 \cdot 10^{-7}\) será: $$ G_{\dot{\theta_{m}}}(s) = \frac{10.994 \cdot 10^{6}}{(s + 68.23)(s + 7.45 \cdot 10^{3})} $$
La función de transferencia para \(B_m = 2.3 \cdot 10^{-6}\) será: $$ G_{\dot{\theta_{m}}}(s) = \frac{10.994 \cdot 10^{6}}{(s + 68.56)(s + 7.45 \cdot 10^{3})} $$
Observando ambas funciones de transferencia podemos ver que no difieren mucho una de la otra. Esto es, se podría utilizar cualquier función de transferenceia para caracterizar el motor y el error sería mínimo con respecto a la otra función de transferencia.
b) Simplificar la función de transferencia por cualesquiera de los métodos que se muestran en los apuntes de la asignatura (25 %).
Para la simplificación de la función de transferencia usaremos dos métodos. El método de eliminación de la constante eléctrica del motor y el método de eliminación del polo no dominante.
Método de eliminación de la constante eléctrica del motor
Podemos escribir la función de transferencia de velocidad angular en la siguiente forma:
$$ G_{\dot{\theta_{m}}}(s) = \frac{K_{m}}{s + p_m} $$
La ganancia a bajas frecuencias del motor será:
$$ G_{\dot{\theta_{m}}}(s) = \frac{k_m}{R_m \ B_m + k_b \ k_m} $$
La función de transferencia del motor, simplificada por este método, tiene un polo de valor:
$$ s = - p_m = - \frac{R_m \ B_m + k_b \ k_m}{R_m \ J_m} = - \frac{1}{t_m} = -\frac{1}{1.48 \cdot 10^{-2}} = - 67.57 $$
Se llega a que:
$$ K_m = p_m \ G_{\dot{\theta_m}}(0) = 67.57 \cdot 21.63 = 1461.43 $$
De esta forma la función de transferencia simplificada será la siguiente:
$$ G_{\dot{\theta_{m}}} = \frac{1461.43}{s + 67.57} $$
Método de eliminación del polo no dominante
Con este método la función de transferencia simplificada será de la forma: $$ G_{\dot{\theta_{m}}} = \frac{K_m}{s + \lvert p_1 \lvert} $$
Podremos calcula \(K_m\) de la siguiente forma: $$ K_m = \frac{k_m}{J_m \ L_m \ \lvert p_1 \lvert} = \frac{4.61 \cdot 10^{-2}}{4.4 \cdot 10^{-6} \cdot 9.53 \cdot 10^{-4} \ \lvert -7.45 \cdot 10^{3} \lvert} = 1475.7 $$
La función de transferencia simplificada será:
$$ G_{\dot{\theta_{m}}} = \frac{1475.7}{s + 68.56} $$