Transductores

Medida de temperatura

Resistencia de Pt

$$ R(T_0 + \Delta T) = R_0 (1 + \alpha_1 t + \alpha_2 t…) \approx R_0 (1 + \alpha t) \\ t = (T_0 + \Delta T) \\ \alpha = 3.9 \cdot 10^-3 \quad [C^{-1}] $$

Resistencias NTC’s

$$ R(T) = A \ e^{B/T} = R_N \ e^{B(\frac{1}{T} - \frac{1}{T_N})} $$

Resistencias PTC’s

$$ R(T) = A + C \ e^{(BT)} $$

Comportamineto en carga de los termistores

$$ R(T_a) = \frac{V_a}{I} \\ P_{joule} = R(T) \ I^2 \Rightarrow \Delta T = \beta \ P_{joule} \\ P_{joule} = G_d \ (T - T_A) + C_t \cdot \frac{d \ (T - T_A)}{d \ T} \\ Z= \frac{C_t}{G_d} $$

En donde: $$ \Delta T \quad \text{autocalentamiento} \\ G_d \quad \text{Conductividad térmica} \\ C_t \quad \text{Capacidad térmica / Inercia térmica} $$

Medida de la deformación

$$ \text{Deformación} \quad \varepsilon_L = \frac{l_{final} - l_{inicial}}{l_{inicial}} = \frac{\Delta l}{l_0} \\ \varepsilon_{T} = -\frac{\Delta d}{d} $$

$$ \text{Efecto de Poisson} \quad \upsilon = -\frac{\varepsilon_T}{\varepsilon_L} $$

$$ \text{Módulo de Young} \quad Y = \frac{F/A}{\varepsilon} $$

Extensímetros

Extensímetros metálicos

Sensibilidad:

$$ S = 1 + 2 \upsilon + \frac{d \ p/p}{\varepsilon} $$

$$ R(\varepsilon) = R_0 \ (1 + S \varepsilon) \\ R_0 = R(\varepsilon = 0) \qquad \text{Máxima sensibilidad} $$

Extensiometros semiconductores

$$ S \approx \frac{d \ p/p}{\varepsilon} = \pi \ Y $$

Sensores capacitivos

$$ C = \frac{\varepsilon_0 \ A}{\frac{d_1}{\varepsilon_1} + \frac{d_2}{\varepsilon_2} + … \frac{d_n}{\varepsilon_n}} \\ A = \quad \text{Área de contacto entre placas} $$

$$ \frac{\Delta C / C}{\Delta d / d} = N \ \frac{1}{1 - N \ \frac{\Delta d}{d}} \\ N = \text{Factor de sensibilidad} = \frac{d_1 + d_2}{d_1 + \frac{d_2}{\varepsilon_2}} $$

En algunos casos se podrá aproxima a: $$ C(\Delta l = 0) = C_0 \\ \text{Sustituyes} \ C_0 \ \text{en} \ C(\Delta L) \\ C(\Delta l) = C_0 (1 - \frac{\Delta l}{l_0}) $$

Sensor capacitivo con una de sus armaduras móvil

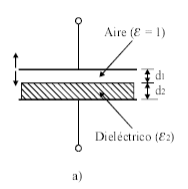
$$ C(d_1) = \frac{\varepsilon_0 \ A}{d_1 + \frac{d_2}{\varepsilon_2}} $$

Sensores inductivos

$$ L = \frac{\mu_0 \ A \ n^2}{\frac{l_1}{\mu_1} + \frac{l_2}{\mu_2} + … + \frac{l_n}{\mu_n}} $$

Sensor entrehierro variable

$$ L = \frac{\mu_0 \ n^2 \ A}{\frac{l}{\mu} + \frac{g}{1}} \\ \Rightarrow L + \Delta L = \frac{\mu_0 \ n^2 \ A}{\frac{l}{\mu} + g - \Delta g} $$

Puente de Wheatstone

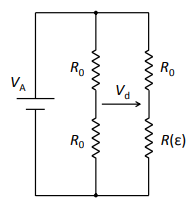
En donde \(V_d\) es la tensión de desequilibrio. Donde por lo general valdrá lo siguiente:

$$ V_d = \frac{V_A}{2} \ \big ( \frac{R(\varepsilon) - R_0 }{R(\varepsilon) + R_0} \big ) $$

Ejemplo de ejercicio temperatura

9.3.- Suponga que las placas metálicas se dilatan en longitud y anchura debido a una variación de temperatura . Escriba la nueva función de transferencia del sensor si el coeficiente de dilatación lineal vale (ºC-1). Calcule el desplazamiento aparente que resultaría para un incremento de temperatura . Realice aproximaciones si lo considera adecuado.

$$ b \Rightarrow b(1 + \alpha \Delta T) \\ l_0 - \Delta l \Rightarrow (l_0 - \Delta l) (1 + \alpha \Delta T) \\ C(\Delta l) = \frac{\varepsilon_0 b (l_0 - \Delta l)}{\frac{d_1}{\varepsilon_1} + \frac{d_1}{\varepsilon_1}} \Rightarrow C(\Delta l, \Delta t) = \frac{\varepsilon_0 b (l_0 - \Delta l)(1 + \alpha \Delta T)^2}{\frac{d_1}{\varepsilon_1} + \frac{d_1}{\varepsilon_1}} \\ C(\Delta l, \Delta T = 0ºC) = \frac{\varepsilon_0 b (l_0 - \Delta l)}{\frac{d_1}{\varepsilon_1} + \frac{d_1}{\varepsilon_1}} \\ C(\Delta l = 0, \Delta T) = \frac{\varepsilon_0 \ b \ l_0(1 + \alpha \Delta T)^2}{\frac{d_1}{\varepsilon_1} + \frac{d_1}{\varepsilon_1}} \\ C(\Delta l, \Delta T = 0ºC) = C(\Delta l = 0, \Delta T) \Rightarrow l_0 - \Delta l_{ap} = l_0 \ (1 + \alpha \Delta T)^2 \\ \Rightarrow \Delta l_{ap} = l_0 \ (1 - (1 + \alpha \Delta T)) $$

Ejercicio de sensibilidad sensor

La sensibilidad de un sensor será un deribada de la magnitud que se mide. Algunos casos son las siguientes:

$$ \text{Condensador armadura fija y movil} \Rightarrow S = \frac{d \ V_d}{d \ g} \\ \text{Extensiometro metálico} \Rightarrow S = \frac{d \ V_d}{d \ F} \\ \text{Medidor de deformación} \Rightarrow S = \frac{d \ V_d}{d \ \varepsilon} $$

Cuando un sensor tiene diferentes sensibilidades se calcula la selectividad comocomo: $$ \text{Selectividad} = \frac{S_1}{S_2} $$

Ejercicio desarrollo de Taylor

Es el ejericio de IELE julio de 2014

$$ R(P) = \frac{R_0}{1 + \frac{P}{P_0}} $$

Obtenga una aproximación lineal de \(R(P)\) para variaciones pequeñas de la potencia \(\Delta P\) alrededor de \(P_0\).

Para obtener \(R(\Delta P)\) tendremos que desarrollar los dos primeros términos del desarrollo en serie de Taylor de la función \(P = P_0 + \Delta P\). De esta forma:

$$ R(\Delta P) = R(P_0) + \frac{d \ R}{d \ P} \bigg \lvert_{P = P_0} \cdot \Delta P \\ = \frac{R_0}{2} - \frac{R_0}{P_0 \cdot (P_0 + P)^2} \cdot \Delta P \\ = \frac{R_0}{2} + \frac{-R_0/P_0}{4} \cdot \Delta P \\ = \frac{R_0}{2} \bigg ( 1 - \frac{\Delta P}{2 \cdot P_0} \bigg ) $$