Ruido en instrumentación
Factor de ruido
Si el amplificador no introduce ruido
$$ \big (\frac{S}{N} \big ){out} = (\frac{S}{N}){in} = \frac{V_{si}^2}{E_{ns}} $$
Si el amplificador si introduce ruido
$$ \big ( \frac{S}{N}\big ){out} = \frac{V_{si}^2}{E_{ns}^2 + \frac{E_{amp}^2}{A_v^2}} < \big ( \frac{S}{N}\big ){in} \qquad ( \frac{S}{N}\big ){in} = \frac{V_{si}^2}{E_{ts}^2} $$
$$ (S/N)out = \frac{V_{s0}^2}{E_{n0}^2} $$
Factor de ruido
$$ F = \frac{(S/N)i}{(S/N)0} \\ \text{Ideal} \Rightarrow \quad F = \frac{E_{ni}^2}{E_{trans}^2} $$
$$ \text{Figura de ruido} \quad NF(dB) = 10 \log(F) $$
Potencia disponible de ruido
$$ P_{joule} = \frac{V_{RMS}^2}{4R_i} = N_T $$
Ancho de banda de ruido
$$ B_n = \frac{1}{A_{V0}^2} \int_{0}^{\infty}{[A_{v}(f)]^2 df} \\ B_n = \frac{1}{H_0} \int_{0}^{\infty}{\lvert H(f) \lvert \ df} $$
Se cumple que:
$$ B_{n_{ruido}} > B_{señal} \\ B_n \approx \frac{\pi}{2} B_S $$
Además si a su entrada tiene un ruido blanco con densidad espectral Sni (V2 /Hz) y ancho de banda Bni (Hz), la potencia de ruido a la salida será:
$$ N_o = A_{v0}^2 \ B_n \ S_{ni} \qquad [V^2] $$
Ruido térmico
$$ E_T^2 = 4 \cdot R \cdot K \cdot T \Delta f \\ S_T = \frac{E_T^2}{\Delta f} = 4 \cdot R \cdot K \cdot T $$
Ruido shot
$$ I_S^2 = 2 \cdot e \cdot I_{DC} \cdot \Delta f \\ S_S = \frac{I_S^2}{\Delta f} = 2 \cdot e \cdot I_{DC} $$
Ruido de baja frecuencia | Ruido flicker
$$ E_{1/f}^2 = k \cdot \ln{\lvert \frac{f_{max}}{f_{min}}\lvert} \\ S_{1/f} = \frac{k}{f^{\alpha}} \ [V^2/Hz] \qquad \alpha \approx 1 $$

Factor de calidad
$$ Q = \frac{f_0}{B_s} \\ B_S \Rightarrow \text{Ancho de banda señal a -3dB} $$
Modelo En-In en un circuito
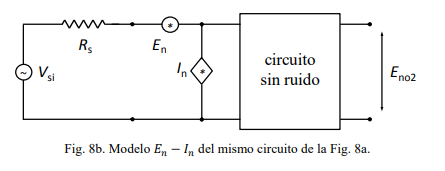
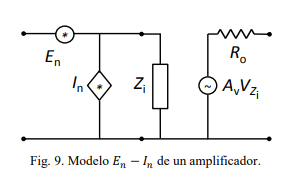
Por cada componente se mete ruido (si procede) y luego se simplifica aplicando transformaciones.
El ruido se transforma así:
- Ruido en serie con otra impendancia se divide
- Ruido en paralelo con otra impedancia se multiplica
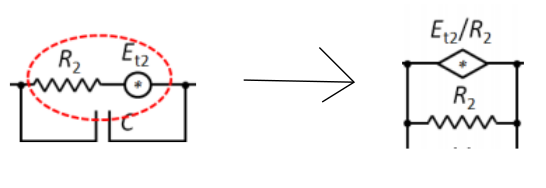
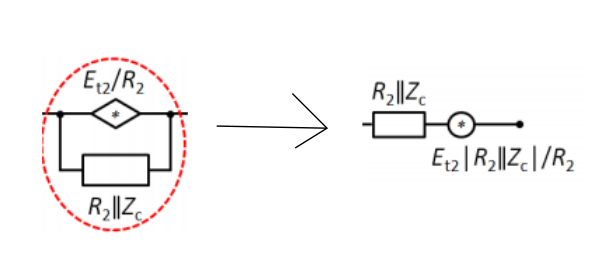
Ejemplo de cálculo:
- Cálculo de la ganancia en tensión. Quitando los generadores de ruido. \( \lvert K_T \lvert = \frac{V_{so}}{V_{si}}\)
- Calculo \(E_{no}\) en general por superposición de todos los generadores de ruido que tengamos, que será ir anulando los otros y ver la salida:
$$
E_{no}^2 = E_{no}(E_{Ts})^2 + E_{no}(E_{Ts})^2 …. \\ E_{no}^2 = \lvert K_T \lvert^2 \ E_{ni}^2
$$
- Calculo \(E_{ni}^2 = \frac{E_{no}^2}{\lvert K_T \lvert^2}\)
- Calculo
$$ F = \frac{(S/N)in}{(S/N)out} = \frac{E_{ni}^2}{E_{trans}^2} $$ $$
Mejora de la SNR
$$ SNRI = \frac{(S/N)out}{(S/N)in} $$
Señal de muy baja frecuencia
$$ SNRI = \frac{B_{ni}}{B_{nFPB}} $$
Ojo cuidao que se está refiriendo al ancho de banda del ruido de entrada partido por el ancho de banda del ruido del filtro, que será \(\frac{\pi}{2} f_{c_{filtro}}\)
Señal de frecuencia intermedia
$$ SNRI = \frac{B_{ni}}{B_{nFPBd}} $$