CUDA

Número máximo de hilos = 512 a repartir entre las 3 dimensiones será el nº de hilos de cada dimensión (x,y,z). Para const dim block_size(nThreads, nThreads, nThreads):

• Dos dimensiones será \( (32,16,1) \Rightarrow 32 \cdot 16 \cdot 1 = 512 \)
• Tres dimensiones será \( (8,8,8) \Rightarrow 8 \cdot 8 \cdot 8 = 512 \)

Número de bloques por cada dimensión:

$$ \text{nBlocksX} = \frac{A_x + (n_x - 1)}{n_x} \\ \text{nBlocksY} = \frac{A_y + (n_y - 1)}{n_y} $$

Siempre redondear hacia abajo.

Tal que \(n_x\) y \(n_y\) es el número de hilos de cada dimensión. Y \(A_x\) y \(A_y\) el número de píxeles de la imagen.

Número de bloques en la ejecución = \(\text{nBlocksX} \cdot \text{nBlocksY}\)

Bloques que procesa cada SM: \(\frac{\text{Nº bloques ejecución}}{nº SMs} = \frac{bloques}{SM}\)

Nº de ciclos proceso = \(\frac{nºciclos}{bloque} \cdot \frac{nºbloques}{nºSMs}\)

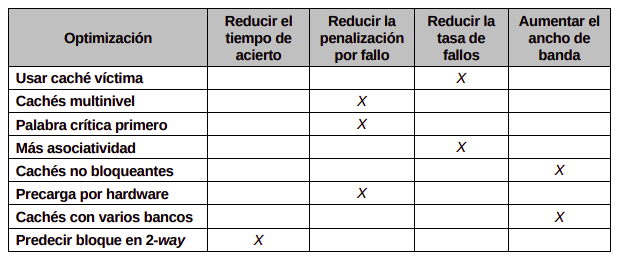
Cachés MRi, MRd, L1, L2 y L3

$$ MR2 = \text{Tasa de fallos} $$

Con write-around desaparece el % de stores

• cachés con búfer de escrituras, write-through y write-allocate para store.

Se suponen cachés write-allocate con búfer de escrituras, con lo que todos los fallos en la caché de datos penalizan, pero no se espera a la actualización de memoria tras los de store.

$$ \text{fallosL1} = MR_I + (MR_D \cdot ( \% \text{store} + \% \text{load})) \\ $$

$$ \begin{align*} & 1 \text{ Caché} \qquad CPI_{real} = CPI_{ideal} + \text{PenalizaciónL1} \cdot \text{fallosL1} \\ & 2 \text{ Caché} \qquad CPI_{real} = CPI_{ideal} + (\text{PenalizaciónL1} + MR2 \cdot \text{PenalizaciónL2}) \cdot \text{fallosL1} \\ & 3 \text{ Caché} \qquad CPI_{real} = CPI_{ideal} + (\text{PenL1} + MR2 ( \text{PenL2} + MR3 \cdot \text{PenL3})) \cdot \text{fallosL1} \end{align*} $$

• Cachés sin búfer de escrituras con write-through

$$ \begin{align*} & 1 \text{ Caché} \qquad CPI_{real} = CPI_{ideal} + \text{PenalizaciónL1} \cdot (MR_I + MR_D \cdot \% \text{load} + \% \text{store}) \end{align*} $$

• Cachés write-back con L1 sin búfer de escrituras y un % son dirty $$ \begin{align*} & 1 \text{ Caché} \qquad CPI_{real} = CPI_{ideal} + \text{PenL1} \cdot (MR_I + MR_D \cdot ( \% \text{store} + \% \text{load}) + MR_D( \% \text{load} + \% \text{store}) \cdot \% \text{dirty}) \\ & 2 \text{ Caché} \qquad CPI_{real} = CPI_{ideal} + \text{PenL1} \cdot (MR_I + MR_D \cdot ( \% \text{store} + \% \text{load}) + MR_D( \% \text{load} + \% \text{store}) \cdot \% \text{dirty}) + (\text{PenL2} \cdot MR2)(MR_I + MR_D(\% \text{store} + \% \text{load})) \end{align*} $$
• Cachés L1 y L2 write-back sin bufer y % son dirty

$$ \begin{align*} & CPI_{real} = CPI_{ideal} + \text{PenL1} \cdot (MR_I + MR_D \cdot ( \% \text{store} + \% \text{load}) + MR_D( \% \text{load} + \% \text{store}) \cdot \% \text{dirtyL1} + \text{PenL2} \cdot MR2 \cdot (1 + \% \text{dirtyL2}) \cdot (MR_I + MR_D \cdot ( \% \text{store} + \% \text{load})) \end{align*} $$ Cuidado con que poner en la penalización de cachés. La penalización por fallo de caché será la de L2 y el tiempo de acceso será la penalización de L1. Lo he visto en algunos ejercicios.

Paralelismo

$$ \text{Paralelismo} = \text{Tasa} \cdot \text{Tiempo de ejecución} \\ \text{Tasa} = \text{nº de unidades funcionales} \\ \text{Latencia media} = \text{Tiempo de ejecución} = \frac{\text{nº unidades} \cdot \text{ciclos} + \text{nº unidades} \cdot \text{ciclos} + …}{\text{nº de unidades}} \\ \text{% ocupación} = \text{Paralelismo_old}/\text{Paralelismo_new} \cdot 100 $$

Predicción de saltos

$$ \text{Instrucciones a descartar por ciclo} = CPI_{stall} \cdot \text{instr. emitidas por ciclo} \\ CPI_{stall} = \text{Ciclos por predicción incorrecta} = \\ (\text{etapa salto} - 1) + \frac{\sum_{i = 0}^{\text{instr emitidas por ciclo - 1}} i / \text{instr emitidas por ciclo}}{\text{Intruscciones emitidas por ciclo}} $$

$$ CPI_{real} = CPI_{ideal} + CPI_{stall} \cdot \% \text{Prob.parada} \\ \% \text{Prob.parada} = \% \text{saltos} \cdot (1 - \% \text{Prob.acierto}) \\ CPI_{ideal} = \frac{1}{\text{instr.emitidas por ciclo}} \\ \text{Speedup} = \frac{CPI_{ideal}}{CPI_{real}} $$

Ejercicio de arquitecturas

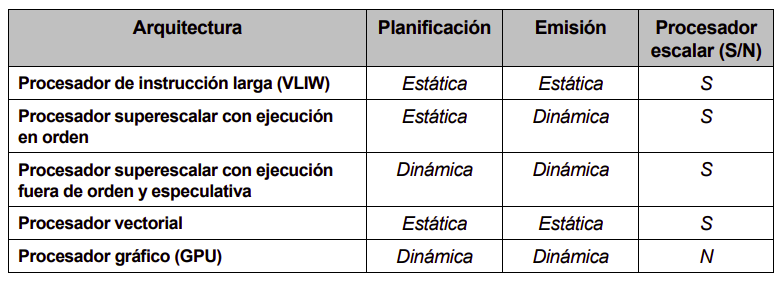
SIMD

$$ \text{Duración } 1 \text{ ciclo de reloj } = \frac{1}{f_{clk}} = [seg/ciclo] \\ \text{Accesos a un banco } = \frac{\text{Tiempo de acceso}}{[\text{seg/ciclo]}} = [\text{ciclos}]\\ \text{Nº de accesos por ciclo} = \frac{\text{nº bancos memoria}}{\text{ciclos}} = [\text{accesos}] \\ \text{Nº de accesos por procesador cada ciclo} = \frac{[\text{accesos}]}{\text{nº procesadores}} $$

Caché

El bueno de bocata ha hecho un super video explicando esto. Lo tienes por aquí la primera parte y luego la segunda parte.

CUIDADO a donde la dirección hace referencia.

Si la referencia es de tipo word: Directamente en base 2 el nº de palabras por bloque.

Si la referencia es de tipo byte: 1 WORD = 4 BYTES.

Caché de mapeo directo

• Indice (index): bits inferiores de la dirección del bloque
• Etiqueta (tag): bits superiores de la dirección del bloque
• Posición = (dirección del bloque) mod (bloques en la caché)
• Tamaño caché \(2^i\) bloques
• Tamaño bloque \(2^b\) bytes

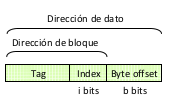La dirección de la linea nos la da index.

Cachés asociativas

Resolverán el problema de acceso alternativo a dos bloques con la misma dirección

Se organizan en grupos (sets) de n líneas con el mismo índice

A medida que crece la asociatividad reduzco fallos pero aumento coste.

Cachés completamente asociativas

Es como una caché asociativa pero sólo hay un único grupo. Con lo que solo tiene tag + offset. NO hay bits de index. Con lo que sólo hace falta calcular el offset.

NUMA

$$ \begin{align*} & \text{Matriz} = (X,Y) \\ & \text{Nº lecturas } = 2 \cdot X \cdot Y\\ & \text{Nº escrituras } = X \cdot Y \\ & \text{Nº lecturas cada nucleo} = \frac{\text{Nº Lecturas}}{\text{Nº procesadores} \cdot \text{Nº nucleos}} \\ & \text{Nº lecturas locales} = \text{Nº lectuas cada nucleo} \cdot \frac{1}{\text{Nº procesadores}} \\ & \text{Nº lecturas remotas} = \text{Nº lecturas cada nucleo} \cdot \frac{\text{Nº procesadores} - 1 }{\text{Nº procesadores}} \\ & \text{Nº de escrituras cada nucleo} = \frac{\text{Nº escrituras}}{\text{Nº procesadores} \cdot \text{Nº nucleos}} \\ \end{align*} $$

Si las matrices están uniformemente distribuidas: $$ T = \text{Ciclos}_{local} \cdot \text{Nº lectura}_{local} + \text{Ciclos}_{remoto} \cdot (\text{Nº lecturas}_{remoto} + \text{Nº escrituras cada nucleo}) $$

Si se lee en unos procesadores y se escribe en otros diferentes: $$ T = \text{Ciclos}_{remoto} \cdot (\text{Nº lecturas cada nucleo} + \text{Nº escrituras cada nucleo}) $$