No idealidades del reloj

• Clock skew: retardo en la señal de reloj siempre con un valor fijo. Normalmente tiene un efecto negativo en circuitos secuenciales síncronos.
• Jitter: retardo con un valor aleatorio

$$ T_{hold} \le T_{cq} + T_{next(min)} - T_{skew} \\ T_{hold} \le T_{cq} + T_{skew} $$

Múltiples relojes

• Independientes
• Derivados
• GALS: Sistema globalmente asíncrono y linealmente síncrono

Meta-estabilidad

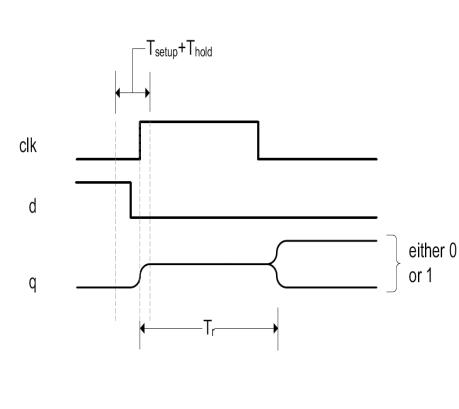
Después de un \(T_r\) (tiempo de resolución) este se pone a 0 o a 1.

El tiempo de resolución es una variable probabilística que define el tiempo que tarda de pasar del valor intermedio a 0 o 1. Se define la función de densidad de probabilidad ¿Cual es la probabilidad que después continue la metaestabilidad?:

$$ P(T_{r}) = e^{\frac{-T_r}{\tau}} $$

Siendo \(\tau\) = Cte de decaimiento del FF

El método para minimizar la probabilidad de metaestabilidad es la utilización de sincronizadores de 2 o más FFs.

MTBF (Tiempo medio entre fallos de sincronización)

Calculamos el reciproco: AF (tasa de fallos por segundo)

$$ AF(T_r) = R_{META} \cdot P(T_r) \\ R_{META} \equiv \text{Tasa media en la que un FF entra en metaestabilidad} \\ R_{META} = \omega \cdot f_{clock} \cdot f_d \\ \omega \equiv \text{ventana susceptible de entrar en metaestabilidad} $$

En un segundo tenemos \(f_{clock}\) flancos de reloj -> luego en 1 segundo tenemos \(\omega f_{clock} (seg)\) susceptibles de metaestabilidad.

$$ f_d \equiv \text{transiciones/seg de la señal de entrada} $$

Habrá \(\omega \cdot f_{clk} \cdot f_d\) transiciones en las ventanas de susceptibilidad.

Solo se producirá error de sincronización cuando alguna de estas transiciones no se haya estabilizado después de \(T_r\). Con lo que llegamos a:

$$ MTBF = \frac{1}{AF(T_r)} = \frac{e^{\frac{T_r}{\tau}}}{\omega \cdot f_{clk} \cdot f_d} $$

Sincronizadores

Sincroniza una entrada asíncrona con el reloj del sistema. Proporciona el suficiente tiempo para resolver la metaestabilidad.

Dónde usar sincronizadores -> Señales libres de glitches en un solo lugar no sincronizar señales que estén relacionadas.

No sincronizador

No hay \(T_r\), en cuanto sale ya se propaga

Caso de sincronizador con un único flipflop

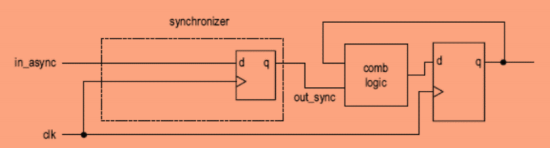
Si el flip-flop del sincronizador entra en metaestabilidad, una vez que se estabilice la señal a su salida, aún tendrá que recorrer la lógica combinacional y llegar antes del tiempo de setup del siguiente flip-flop para evitar que se propague el estado inestable a través del resto del sistema:

$$ T_r \le T_{clock} - T_{comb} - T_{setup} - T_{skew} $$

Caso de sincronizador con dos flip-flops

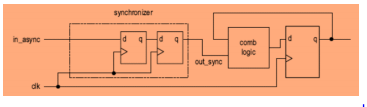
$$ T_r \le T_{clock} - T_{setup} - T_{skew} $$

Caso de sincronizador con tres flip-flops

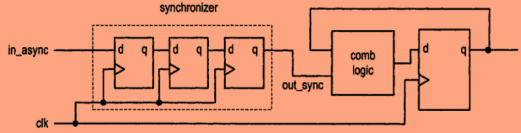
$$ T_r \le 2 \cdot (T_{clock} - T_{setup}) - T_{skew} $$

Frecuencia máxima de funcionamiento

Cálculo de periodo de reloj mínimo:

$$ T_{c(min)} = T_{cq} + T_{next(max)} + T_{setup} + T_{skew} \\ T_{cq} = T_{cqFF} = T_{propFF} \\ T_{next(max)} = T_{comb(max)} $$

\(T_{cq}\) se referirá al flipflop de la señal de entrada, y luego \(T_{setup}\) se referirá al siguiente fliflop. Para que afecto el \(T_{skew}\) tiene que salir la señal de un flipflo y entrar en otro distinto.

La operación anterior se hace siguiendo el peor camino posible.

Si sólo hay un FF involucrado no hay \(T_{skew}\)