Parte A

El objetivo de esta parte de la práctica es diseñar un filtro paso bajo (LP) mediante la conexión en cascada de etapas de primer y segundo orden.

Las características del filtro que se debe diseñar son:

• Respuesta tipo Chebyshev
• Rizado máximo: Amax = 1 dB
• Frecuencia de corte superior: fH = 20 KHz
• Atenuación a 2fH de al menos 45 dB
• Ganancia: |H0LP|= 0 dB

1

1-Utilizando la tabla 4.1 del libro de Sergio Franco, obtenga el orden necesario para el filtro, así como los parámetros f0 y Q de cada una de las etapas.

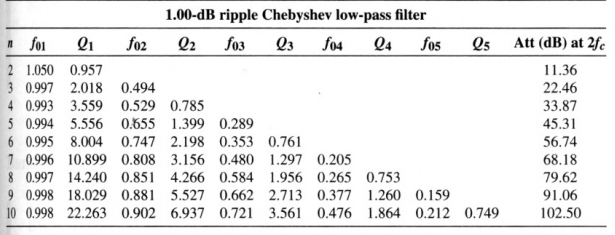
Diseñe el filtro completo, utilizando la estructura de Sallen-Key para las etapas de segundo orden. Elija la opción de ganancia unidad en la etapa de Q más alto y la opción de componentes iguales para las restantes etapas de segundo orden. Las etapas se ordenarán priorizando el margen dinámico en la entrada. Una vez obtenidos los valores nominales de los componentes, utilice valores normalizados del 1% para las resistencias y del 5% para los condensadores.

Usando la tabla y con las condiciones propuestas podemos determinar que el número de etapas del filtro será de 5:

$$n = 5 \\ f_{01} = 0.994 \ Hz \\ Q_1 = 5.556 \\ f_{02} = 0.655 \ Hz \\ Q_2 = 1.399 \\ f_{03} = 0.289 \ Hz$$

Utilizando la transformación de paso bajo: $$f_0 = f_c \cdot f_{0LP_{tabla}}$$

De esta forma llegamos a que: $$f_{01} = 0.994 \cdot 20 \cdot 10^3 = 19.88 \ KHz \\ f_{02} = 0.655 \cdot 20 \cdot 10^3 = 13.10 \ KHz \\ f_{03} = 0.289 \cdot 20 \cdot 10^3 = 5.78 \ KHz \\ $$ Como el filtro es de orden impar, con lo que habrá tendrá 2 etapas de segundo orden y una de primer orden.

Para proporcionar el mejor márgen dinámico de entrada se dispondrán las etapas de menor a mayor Q.

Tal que se nos quedarán las siguientes etapas:

Etapa 1

$$f_{03} = 0.289 \cdot 20 \cdot 10^3 = 5.78 \ KHz \\ $$

Etapa 2

$$f_{02} = 0.655 \cdot 20 \cdot 10^3 = 13.10 \ KHz \\ Q_{2} = 1.399$$

Etapa 3

$$f_{01} = 0.994 \cdot 20 \cdot 10^3 = 19.88 \ KHz \\ Q_{1} = 5.556$$

Diseño etapa 1

Se tratara de una etapa de primer orden que consistirá en un filtro paso bajo de ganancia unidad. Tendremos en cuenta la siguiente ecuación: $$f_{03} = \frac{1}{2 \cdot \pi \cdot R_2 \cdot C} \qquad G_3 = - \frac{R_2}{R_1}$$

Fijamos el valor del condensador para determinar el valor de la resistencia. Quedaría de la siguiente forma: $$C = 10 \ nF \\ R_1 = R_2 = \frac{1}{2 \cdot \pi \cdot f_{03} \cdot C} = \frac{1}{2 \cdot \pi \cdot 5.78 \cdot 10^3 \cdot 10 \cdot 10^{-9}} = 2.754 \ K\Omega$$

El valor normalizado de la resistencia quedaría como: $$R_{norm} = 2.754 \ K\Omega \cdot 0.01 + 2.754 \ K\Omega =2.781 \ K\Omega$$

El valor normalizado del condendador será el valor que le hemos fijado previamente.

Diseño etapa 2

Por ser una etapa de segundo órden seguiremos la estructura Sallen-Key. Utilizaremos el criterio de componentes iguales.

$$R_1 = R_2 = R \qquad C_1 = C_2 = C \\ H_{0LP} = k \qquad k = 3 - \frac{1}{Q} \\ R \cdot C = \frac{1}{\omega_0} \qquad R_B = (k - 1)\cdot R_A$$

Fijaremos el valor de una de las componentes de la siguiente forma: $$C = 10 \ nF$$

Para calcular el valor de R procederemos de la siguiente forma: $$R = \frac{1}{\omega_0 \cdot C} = \frac{1}{2 \cdot \pi f_{02} \cdot C} = \frac{1}{2 \cdot \pi \cdot 13.1 \cdot 10^3 \cdot 10 \cdot 10^{-9}} = 1215 \ \Omega$$

Como nos dicen que las resistencias tienen que estar normalizadas al 1%, la resistencia normalizada se nos quedará como:

$$R_{nom} = 1215 \ \Omega \cdot 0.01 + 1215 \ \Omega = 1227 \Omega$$

Fijaremos el valor de $R_A$ con un valor comercial típico tal que:

$$R_A = 1 \ K \Omega$$

Por lo que $R_B$ quedaría de la siguiente forma:

$$k = 3 - \frac{1}{Q_2} = 3 - \frac{1}{1.399} = 2.29 \\ R_B = (k - 1) \cdot R_A = (2.29 - 1) \cdot 1 \cdot 10^3 = 1.290 \ K \Omega$$

Normalizando el valor de las resistencias un 1% y el valor de los condensadores un 5%: $$C_{norm} = 10 \ n F \\ R_{Anorm} = 1 \ K \Omega \ R_{Bnorm} = 1.290 \ K \Omega \cdot 0.01 + 1.290 \ K \Omega = 1.3 \ K \Omega$$

El filtro tendrá una ganancia de $k = 2.29$ con lo que habrá que corregirla de la siguiente forma:

$$A_{new} = \frac{R_{1B}}{R_{1A}+R_{1B}} \qquad R_1 = R_{1A}//R_{1B} \\ R_{1A} = R_1 \frac{A_{old}}{A_{new}} \qquad R_{1B} = \frac{R_1}{1-A_{new}/A_{old}}$$

Queremos lograr que la ganancia del filtro sea la unidad, con lo que $A_{new} = 1$. Con lo que obtenemos lo siguiente.

$$R_{1A} = R_1 \frac{2.29}{1} = 2776.3 \ \Omega \\ R_{1B} = \frac{R_1}{1 - 1/2.29} = 2156.9 \ \Omega$$

Normalizando el valor de las resistencias al 1% llegamos a lo siguiente: $$R_{1Anorm} = 2776.3 \ \Omega \cdot 0.01 + 2776.3 \ \Omega = 2804 \ \Omega \\ R_{1Bnorm} = 2156.9 \ \Omega \cdot 0.01 + 2156.9 \ \Omega = 2178.5 \ \Omega$$

Diseño etapa 3

Por ser una etapa de segundo órden seguiremos la estructura Sallen-Key. Al ser la etapa con mayor Q utilizaremos la opción de ganancia unidad.

$$R_2 = R \qquad R_1 = m \cdot R \\ C_2 = C \qquad C_1 = n \cdot C \\ \omega_0 = \frac{1}{\sqrt{m \cdot n} \cdot RC} \\ Q = \frac{\sqrt{m \cdot n}}{m + 1} \qquad n \ge 4 \cdot Q^2$$

Fiajmos el valor de C para poder sacar el resto de componentes:

$$C = 1 \ nF \\ 4 \cdot Q^2 = 4 \cdot (5.556)^2 = 123.5 \\ \text{Elegimos } n = 125 \gt 4 \cdot Q^2 \\ Q = \frac{\sqrt{m \cdot n}}{m + 1} \Rightarrow m = 1.25$$

Para determinar el valor de las resistencias procedemos de la siguiente forma:

$$\omega_0 = \frac{1}{\sqrt{m \cdot n} \cdot RC} \\ \Rightarrow R = \frac{1}{2 \pi \cdot f_{01} \cdot C \cdot \sqrt{m \cdot n}} = \frac{1}{2 \pi \cdot 19.88 \cdot 10^3 \cdot 1 \cdot 10^{-9} \cdot \sqrt{1.25 \cdot 125}} = 640.5 \ \Omega$$

Con lo que llegamos los siguientes valores de los componentes:

$$R_1 = m \cdot R = 800.6 \ \Omega \\ R_2 = R = 640.5 \ \Omega \\ C_1 = n \cdot C = 125 \ n F \\ C_2 = C = 1 \ nF$$

Normalizamos estos valores, las resistencias con un 1% y los condensadores con un 5% quedando:

$$R_{1norm} = 800.6 \cdot 0.01 + 800.6 = 808.6 \ \Omega\\ R_{2norm} = R_{norm} = 640.5 \cdot 0.01 + 640.5 = 646.9 \ \Omega \\ C_{1norm} = 125 \ n F \cdot 0.05 + 125 \ n F = 126.25 \ n F$$

Simule en PSPICE el filtro diseñado con los valores normalizados de componentes. Utilice el modelo de amplificador operacional ideal (Parts: OPAMP, con VCC = ±15V). Represente la función de transferencia de cada etapa y del filtro total (módulo y fase). Obtenga la frecuencia de corte superior del filtro (fH), y su ganancia en la banda de paso (H0LP).

Etapa 1

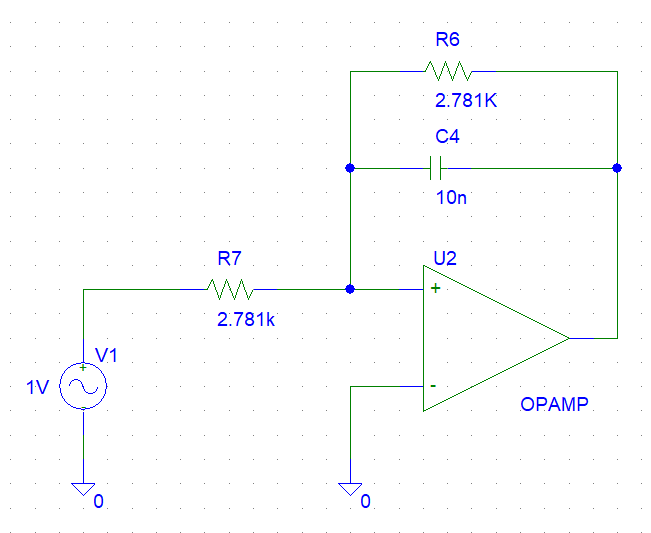
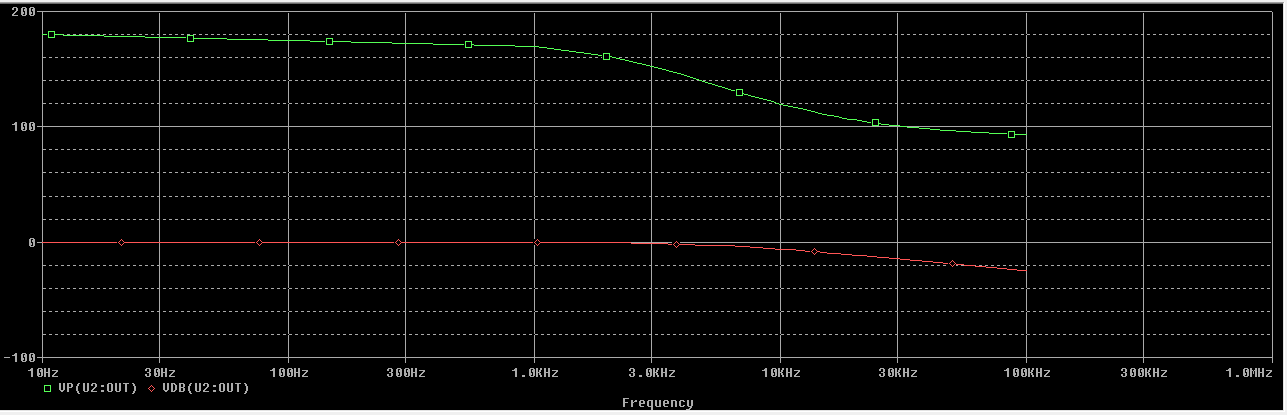
En la que podemos ver que la frecuencia de corte del filtro paso bajo está en $f_{03} = 5.78 \ KHz$

Etapa 2

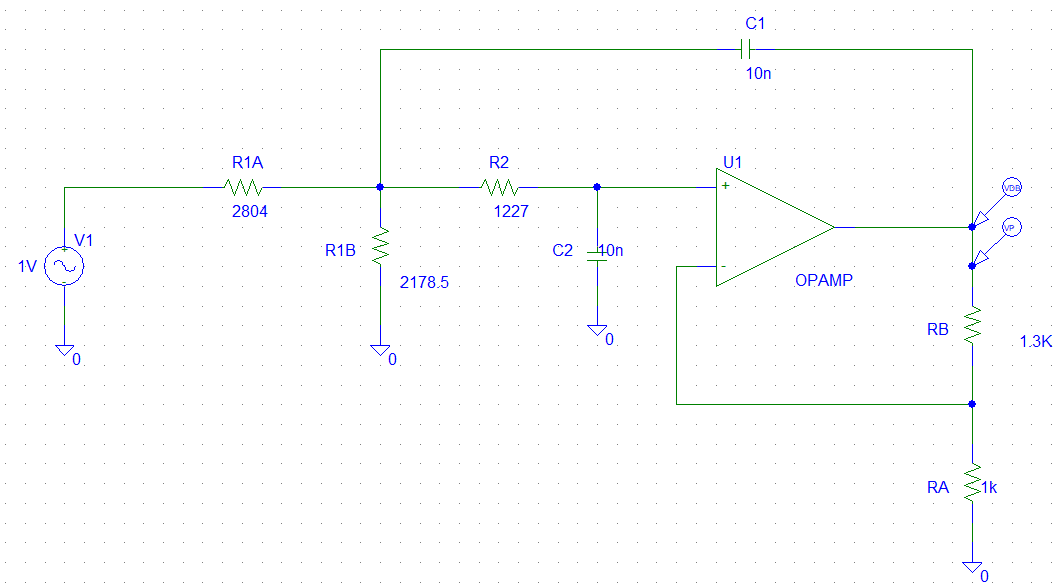
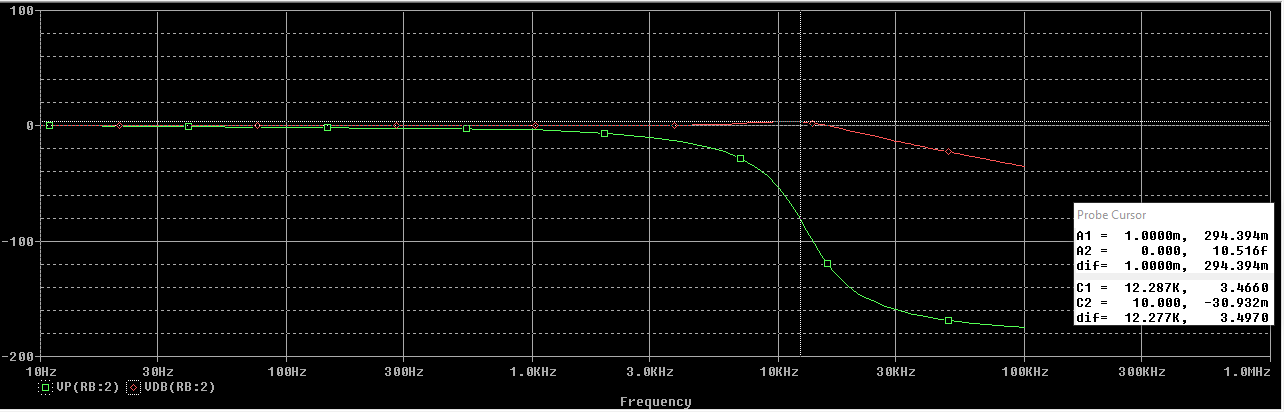
Etapa 3

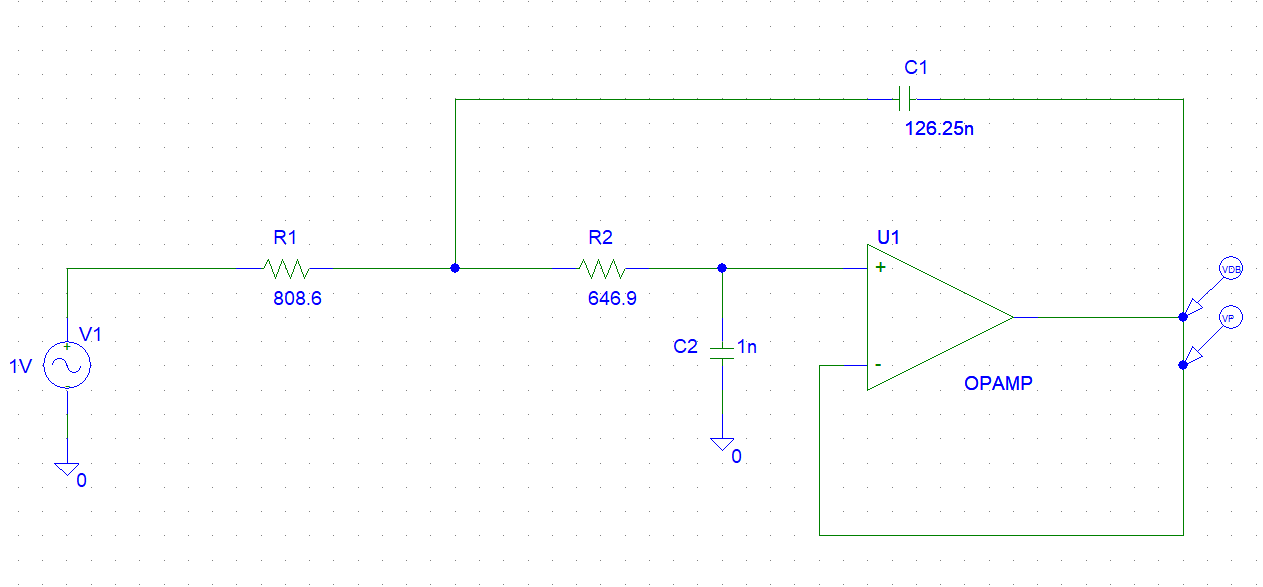
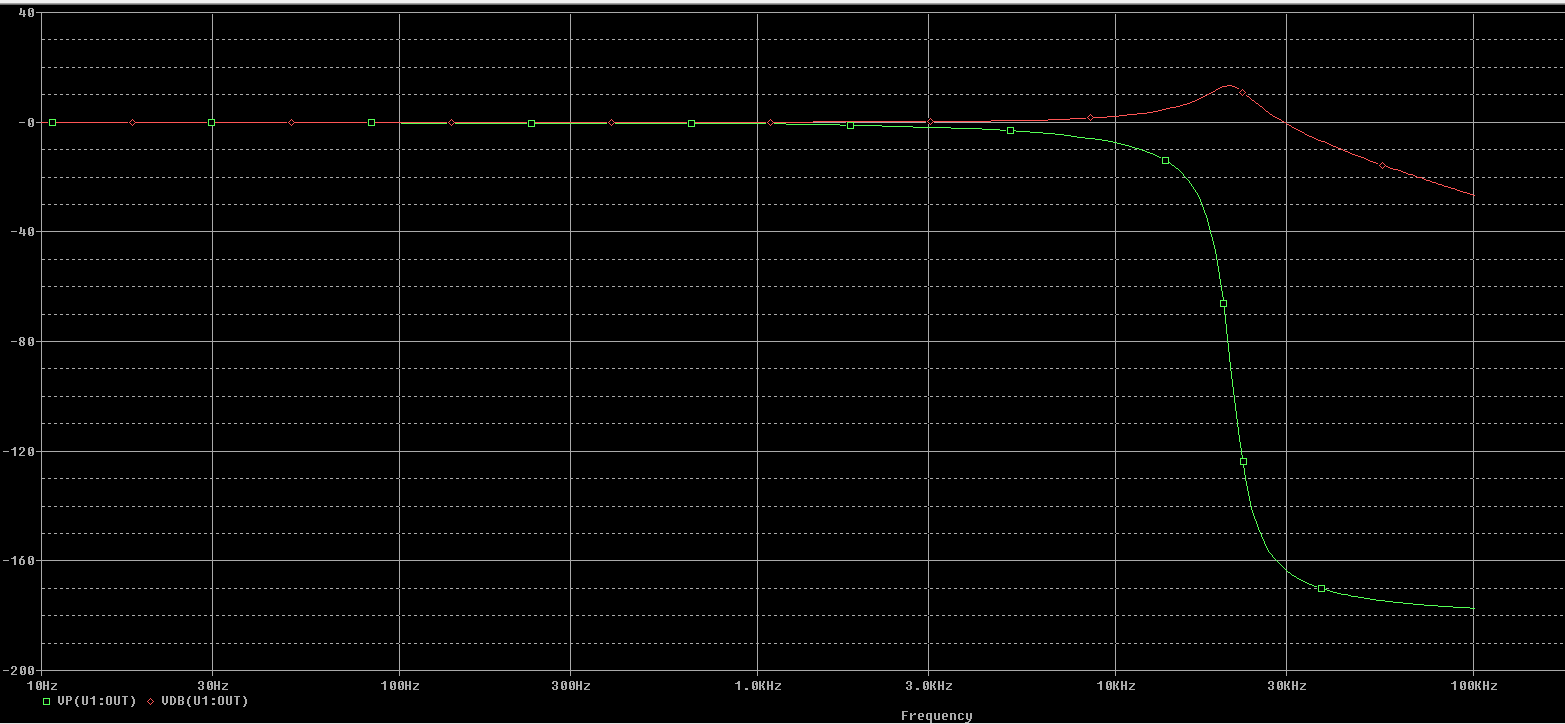
Filtro total

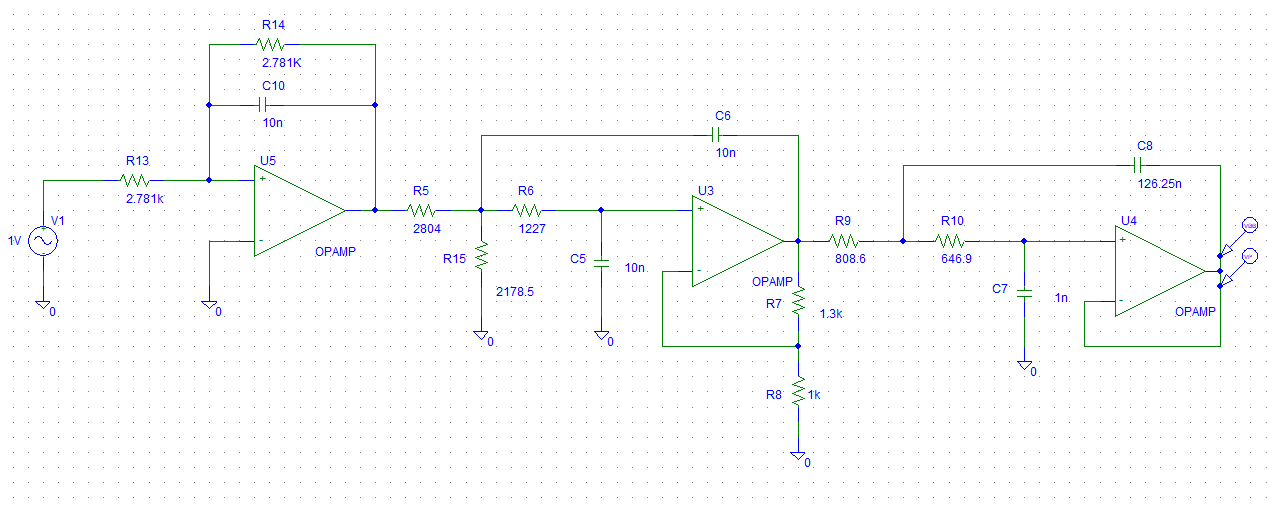
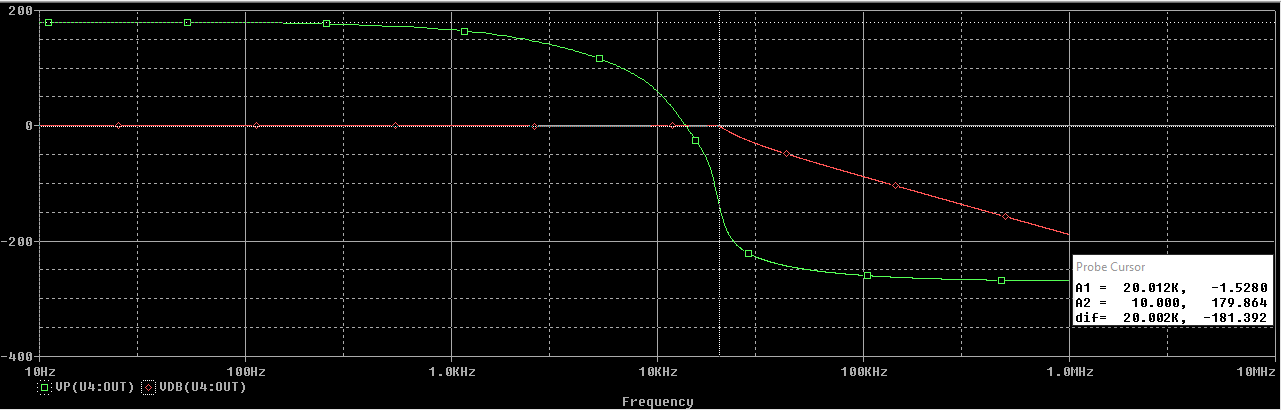
En el marcador se puede ver que la frecuencia de corte del filtro está a 20 kHz. Además, la ganancia en la banda de paso se de 0 dB.

2

Los fabricantes de componentes analógicos suelen ofrecer herramientas de diseño de filtros, adecuadas a los productos de su catálogo. A modo de ejemplo, puede utilizar Filter Wizard, de Analog Devices.

Utilice la herramienta anterior para diseñar el filtro de la práctica, comparando el resultado con el obtenido en el apartado anterior. Tenga en cuenta que en la última pestaña (Next Step) puede elegir la opción “Get Files”, donde tendrá la opción de descargar el fichero DesignFiles.zip con todos los gráficos y resultados relevantes del diseño para incluir en la memoria los que considere más relevantes.

—

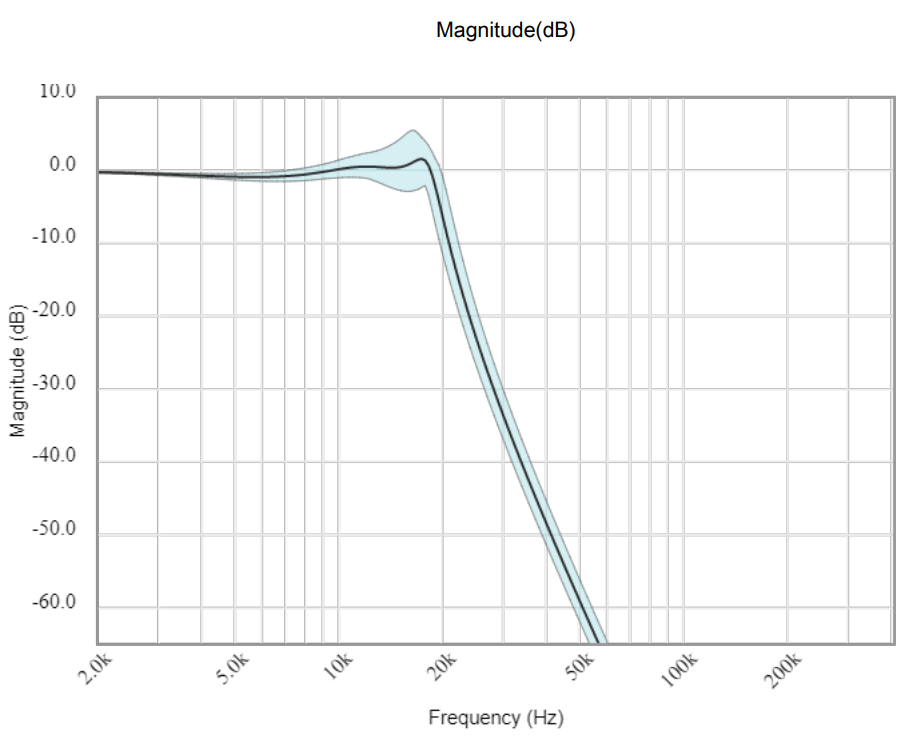
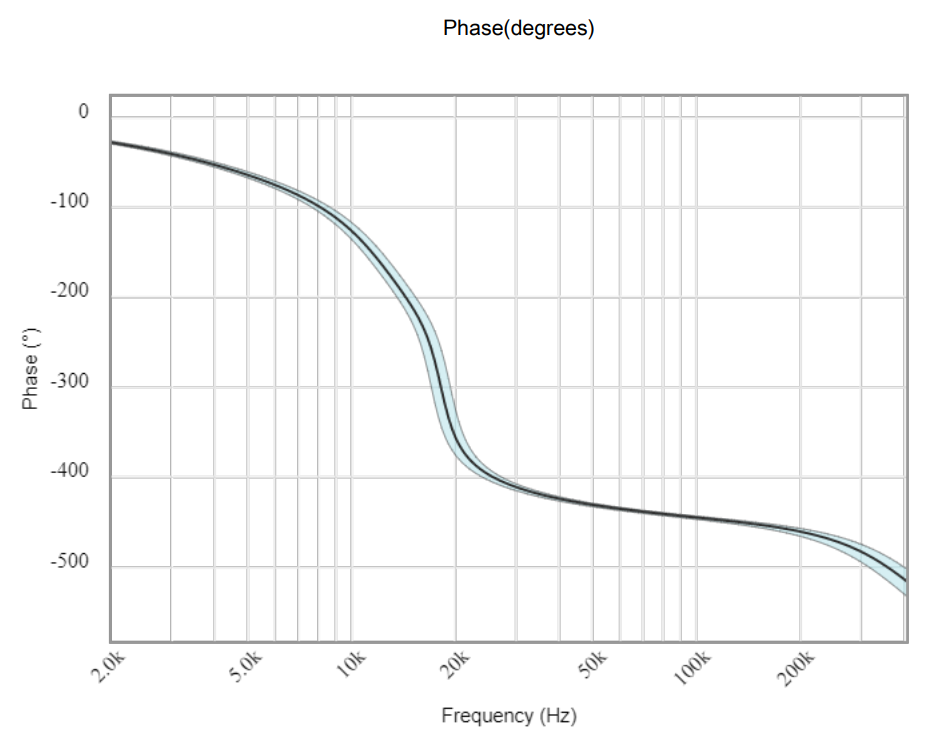
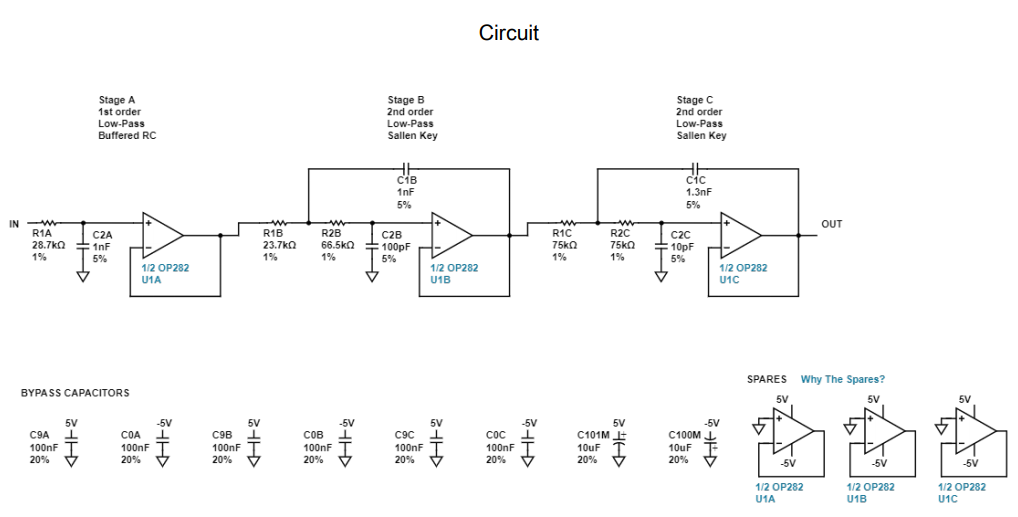Parte B

En esta segunda parte de la práctica se desea realizar la simulación en PSPICE de etapas de salida Clase B realizadas con transistores bipolares. Para ello utilice como referencia la simulación de la etapa clase AB bipolar (fichero claseAB_bipolar.sch). Se estudiarán dos versiones del circuito: etapa clase B pura y etapa clase B con realimentación (configuración seguidor de tensión), con una resistencia de carga RL = 8 Ω. Para el circuito realimentado con amplificador operacional, se empleará el modelo OPAMP, con Vcc = ±12 V.

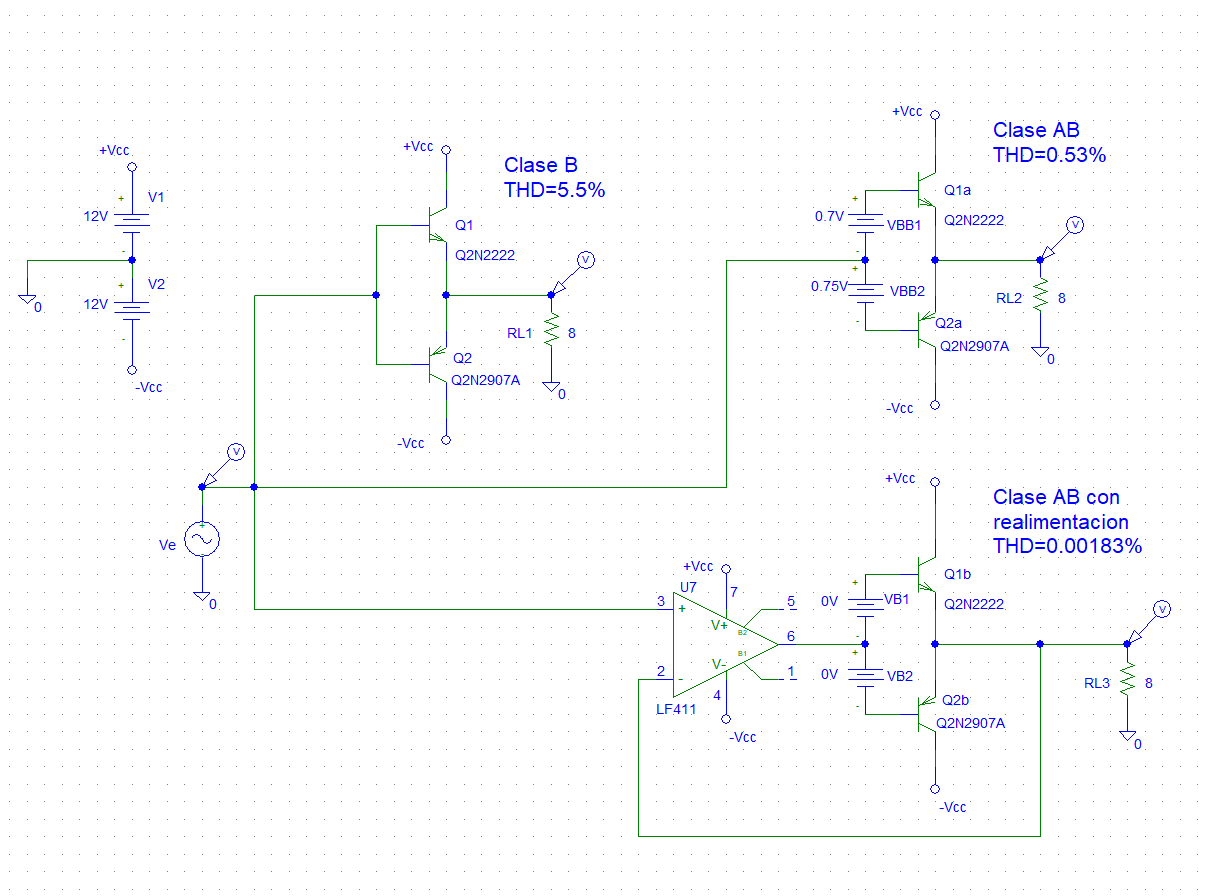
Adaptamos el ejemplo a los datos del enunciado:

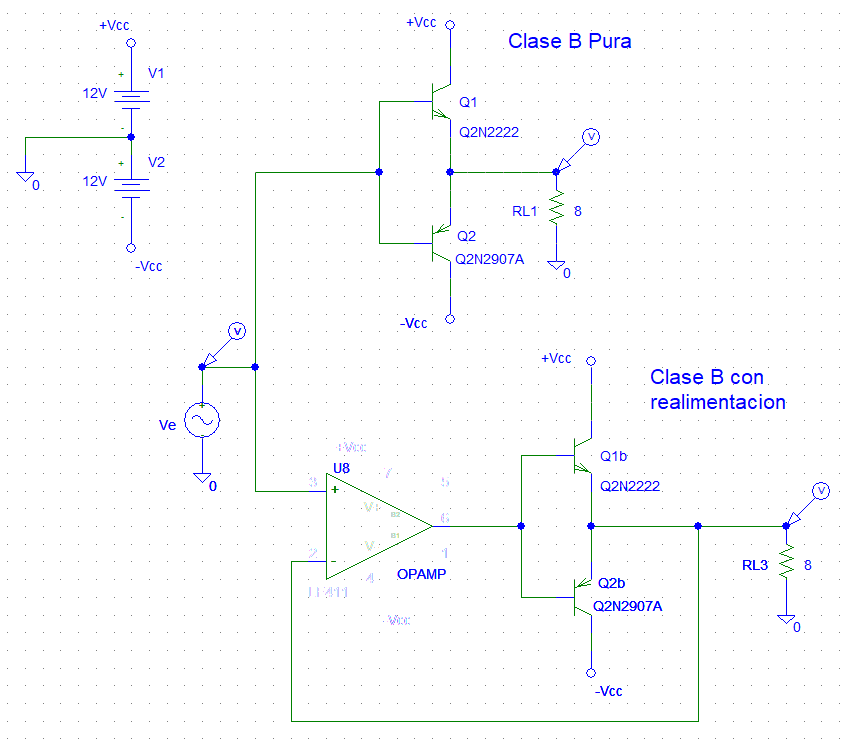
1- Suponiendo que el AO es ideal en todos los parámetros, excepto en la ganancia diferencial, Avd, que será finita, obtenga la expresión de la tensión de salida en la carga de la etapa realimentada. Represente la curva de transferencia entrada-salida.

Para obtener la expresión de la tensión de salida en la carga de la etapa realimentada trendremos en cuenta la ganancia diferencia del amplificador operacional. La tensión de salida del AO, $V_A$:

$$V_A = A_{vd}(V_p - V_n) = A_{vd}(V_I - V_L)$$

Realizando el análisis del circuito obtenemos las siguientes ecuaciones: $$V_L = 0 \quad \text{ cuando } \quad -V_{BE} < A_{vd}(V_I - V_L) < V_A \\ V_L + V_{BE1} = V_{vd}(V_I - V_L) \quad \text{ cuando } \quad A_{vd}(V_I - V_L) > V_BE \\ V_L - V_{BE2} = V_{vd}(V_I - V_L) \quad \text{ cuando } \quad -V_{BE} > A_{vd}(V_I - V_L)$$

De esta forma sacamos los distintos ciclos de trabajo:

Ciclo positivo

En este caso $Q_1$ en activa y $Q_2$ cortado

$$A_{vd}(V_I - V_L) = V_{BE1} + V_L \Rightarrow \\ V_L = V_I \cdot \frac{A_{vd}}{1 + A_{vd}} - \frac{V_{BE1}}{1 + A_{vd}}$$

Ciclo negativo

En este caso $Q_1$ cortado y $Q_2$ en activa

$$A_{vd}(V_I - V_L) = -V_{BE2} + V_L \Rightarrow \\ V_L = V_I \cdot \frac{A_{vd}}{1 + A_{vd}} + \frac{V_{BE2}}{1 + A_{vd}}$$

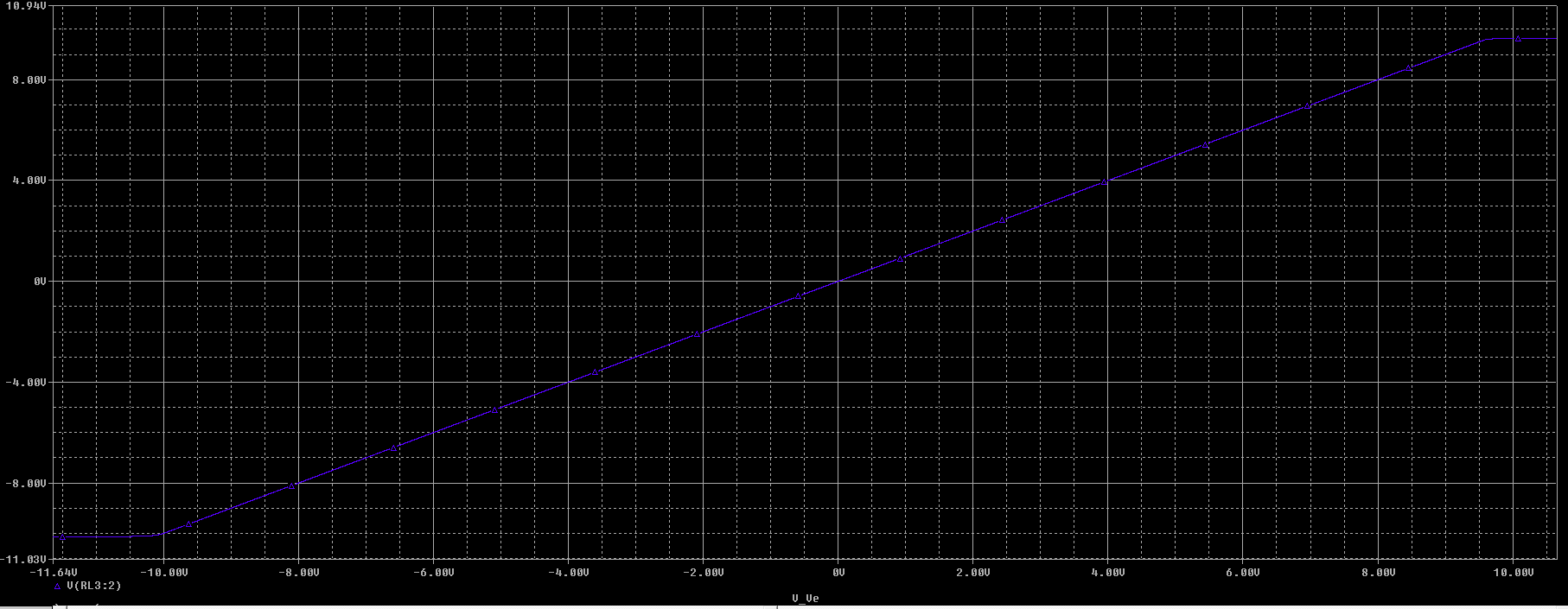
Curva de transferencia de entrada-salida circuito realimentado

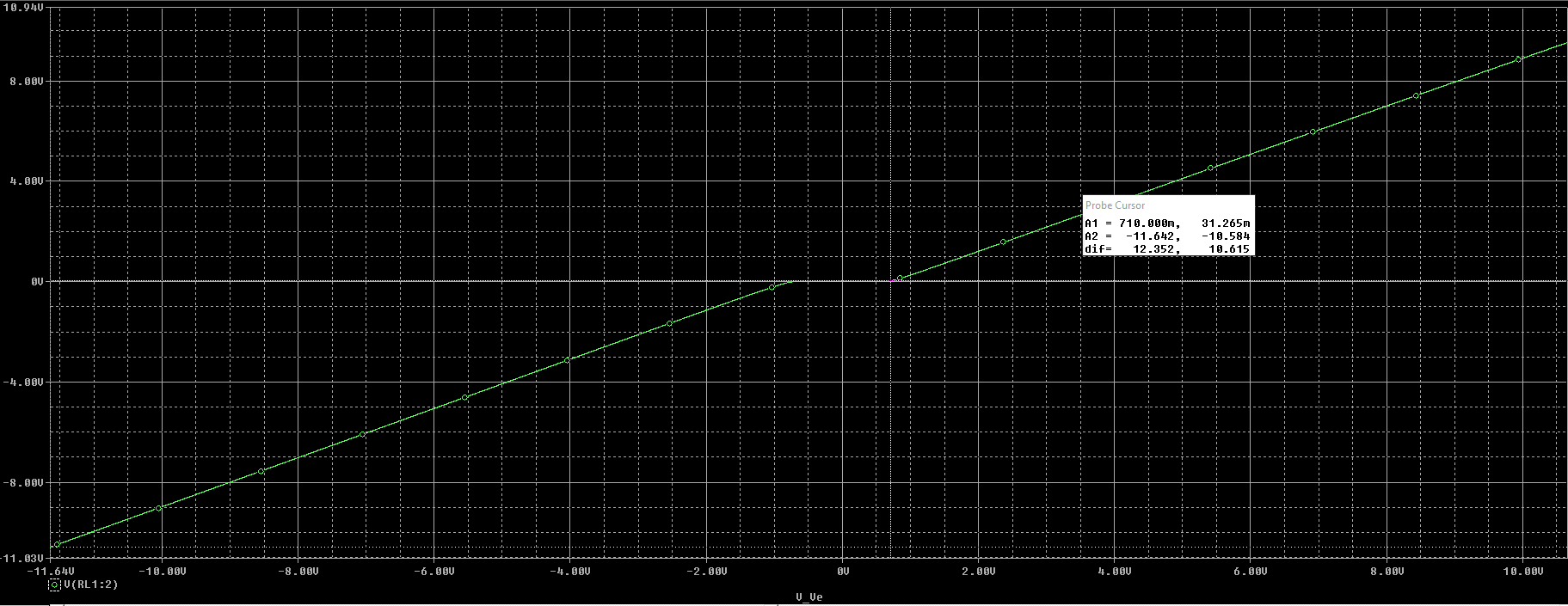
Curva de transferencia de entrada-salida circuito no realimentado

En la gráfica del circuito realimentado podemos ver que se estabiliza tanto por la derecha como por la izquierda en:

$$V_{L_{max}}^+ = V_{OH} - V_{BE1} = V_{OH} - 0.7 = 12 - 0.7 \approx 11.3 V \\ V_{L_{max}}^- = - (V_{OL} + V_{BE2}) = - (V_{OL} + 0.7) = 12 - 0.7 \approx - 11.3 V$$

Para calcular $A_{vd}$ despejamos de de la gráfica de la etapa no realimentada:

$$V_L = 0 \quad \text{cuando} \quad -V_{BE} < A_{vd}(V_I - V_L) < V_A \\ V_I = \frac{V_{BE1}}{A_{vd}} = \frac{0.7}{A_{vd}}$$

Con la ecuación anterior y viendo la gráfica de la etapa no realimentada podemos determinar que:

$$A_{vd} \approx 1$$

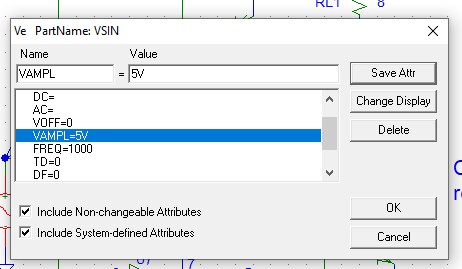
2- Simulación en PSPICE con una señal de entrada sinusoidal (generador tipo VSIN), con 5 V de amplitud y f = 1 kHz. Cada etapa irá alimentada con Vcc = ±12 V.

He han cambiado las propiedades del generador Ve para satisfacer las condiciones del enunciado:

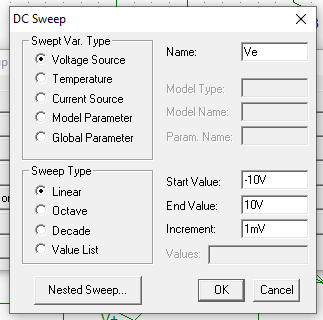
Simulación con barrido DC (DC Sweep: curvas de transferencia entrada-salida). 2.a Utilice como variable de entrada la tensión de excitación. Represente el resultado de la simulación en la salida de las dos etapas (clase B y clase B con realimentación) para una variación de la tensión de entrada de ±10 V y Avd = 10^4 V/V (parámetro GAIN del modelo OPAMP). Para analizar el efecto de la ganancia finita del AO, repita la simulación de la etapa realimentada utilizando Avd = 10^2 V/V. Compare los resultados de la simulación con los previstos por la expresión obtenida en el apartado 1.

Hemos cambiado la variación de tensión de entrada a $\pm 10 \ V$

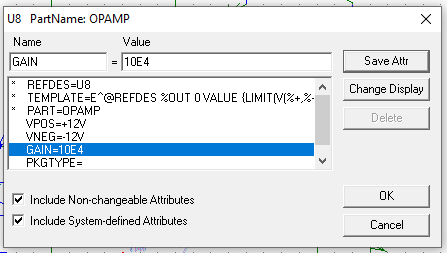
Luego hemos modificador el valor $A_{vd} = 10^4 \ V/V$ del parámetro GAIN del OPAMP:

Simulamos el siguiente circuito:

Para $A_{vd} = 10^4 \ V/V$ obtenemos los siguientes resultados:

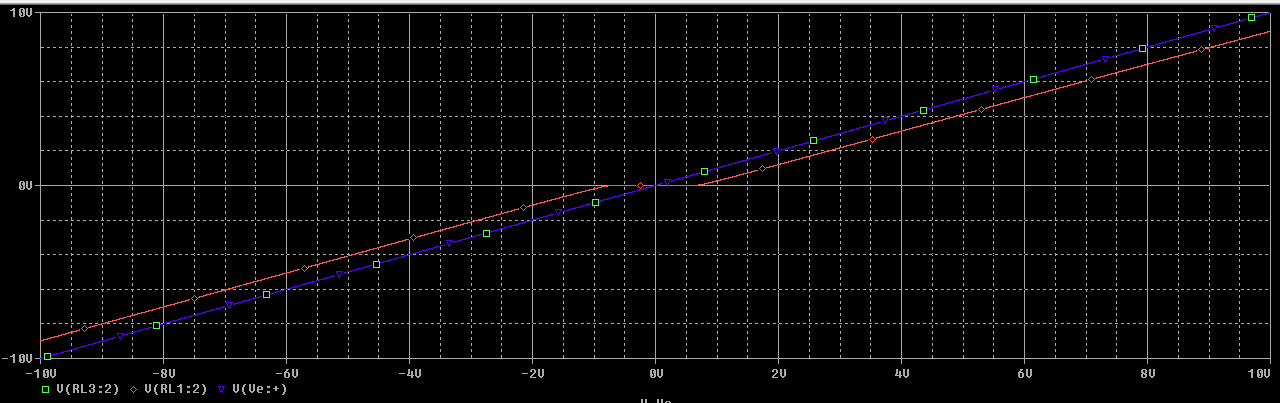
Siendo la verde (solapada por la azul) la gráfica de la etapa realimentada, y la gráfica roja la que no.

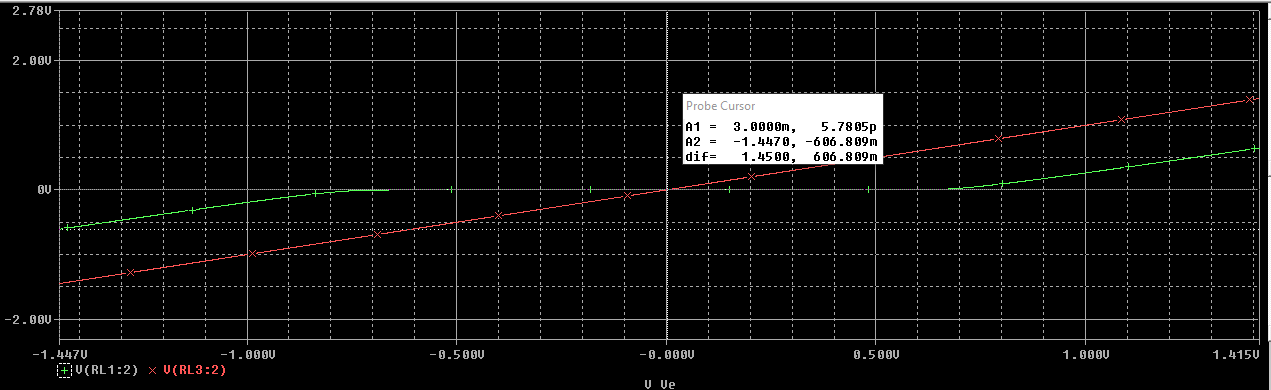
Haciendo zoom podemos determinar que la tensión de cruce es de $3 \ mV$.

Ahora simularemos para el caso de $A_{vd} = 10^2 \ V/V$

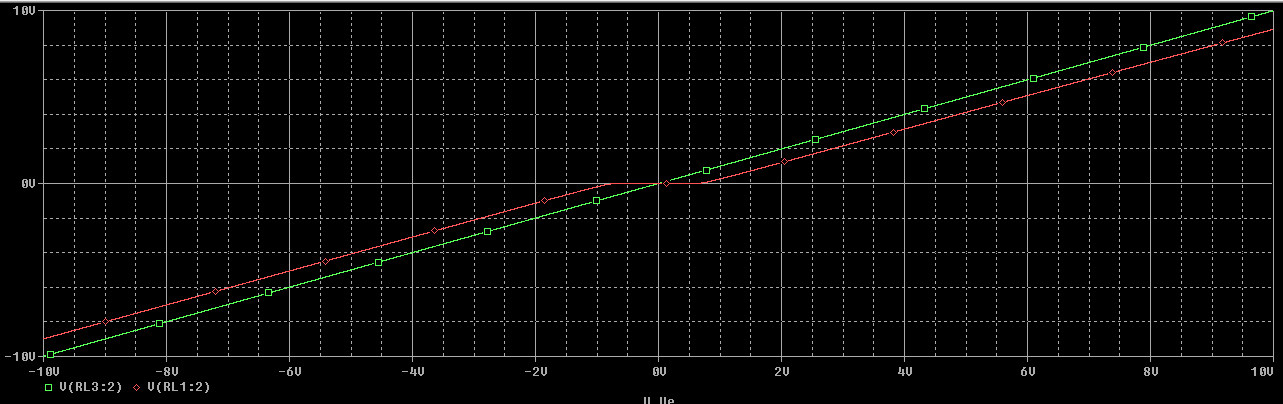
En el que la gráfica roja será la etapa no realimentada, y la gráfica ver la etapa realimentada.

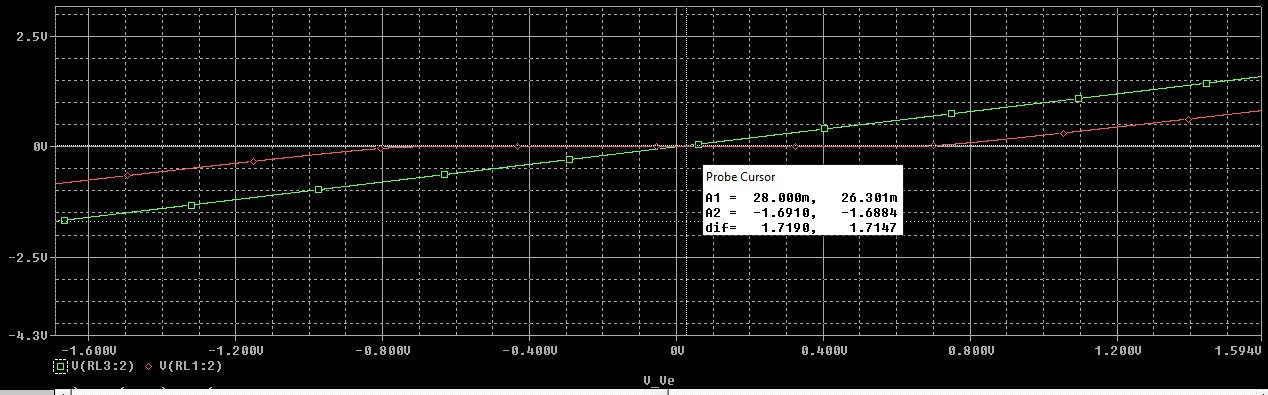
Haciendo zoom podemos determinar que la tensión de cruce es de $28 \ mV$

Comparando los resultados podemos determinar que cuanto mayor sea $A_{vd}$ menor será la tensión de cruce.

La expresión obtenida anteriormente es la siguiente:

$$V_I = \frac{V_{BE1}}{A_{vd}} = \frac{0.7}{A_{vd}}$$

Por lo que se cumple lo que acabamos de obtener en las simulaciones.

• Análisis transitorio. 2.b Simule la etapa sin realimentación y la realimentada con Avd = 10^6 y 10 (V/V); obtenga la distorsión armónica total (THD), activando la opción “Enable Fourier” en la pestaña de configuración del análisis transitorio. Comente los resultados obtenidos, especialmente las diferencias en relación a la amplitud, distorsión de cruce y THD(%).

Para esta parte utilizaremos el análisis transitorio:

Para $A_{vd} = 10^6 \ V/V$

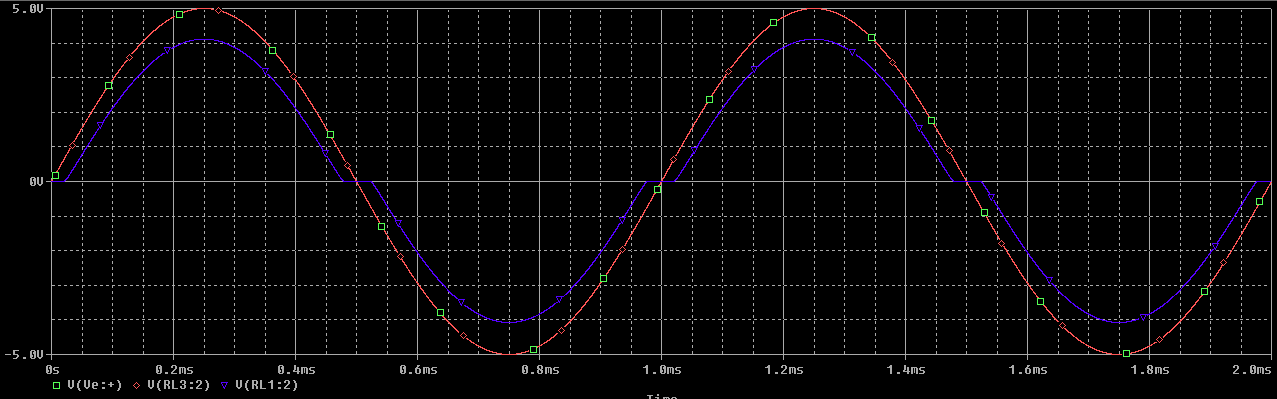
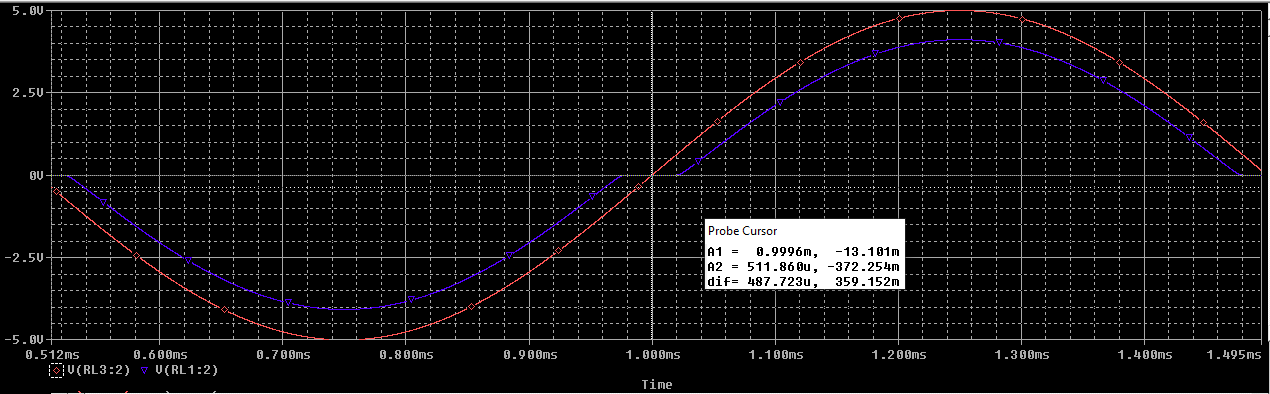
Donde la gráfica roja reprensenta la etapa realimentada y la azul la no realimentada.

Para $A_{vd} = 10 \ V/V$ será lo siguiente:

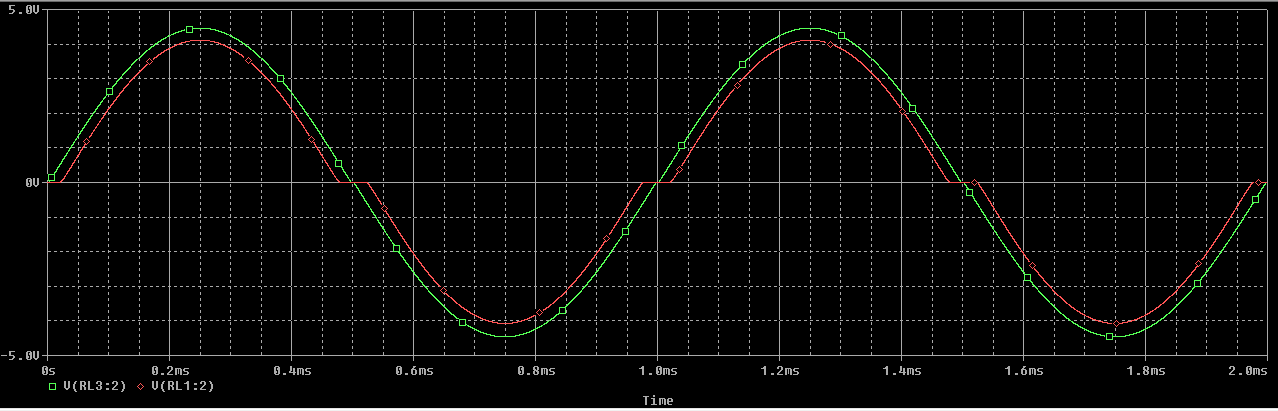
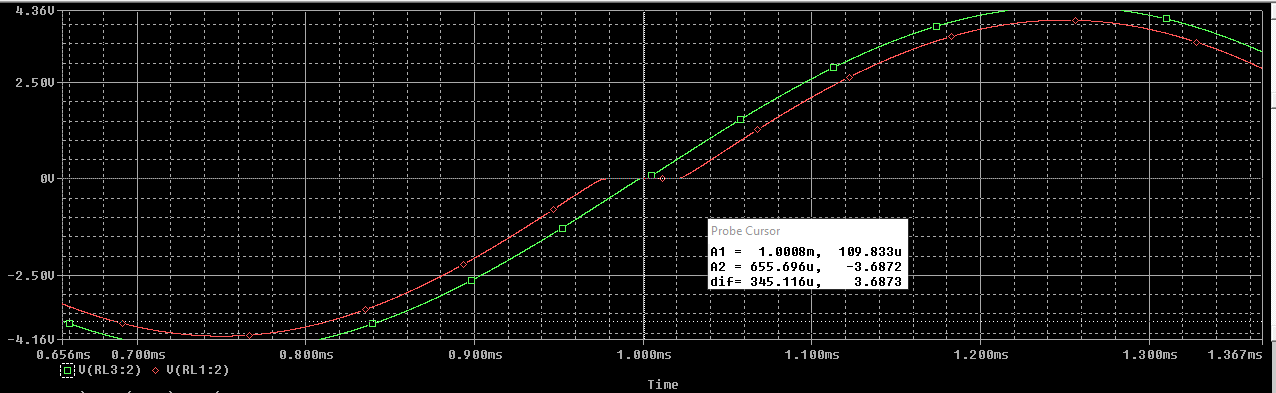
Comparando las dos gráficas podemos ver las diferentes amplitudes de las etapas realimentada y no realimentada. En el caso de $A_{vd} = 10^6 \ V/V$ se puede ver que la diferencia entre las amplitudes de las etapas es considerablemente menor que en el de $A_{vd} = 10 \ V/V$.

2.c En la versión realimentada, (con Avd = 10^6 y 10 V/V), represente la potencia media entregada a la carga, la potencia media entregada por las fuentes de alimentación y estime el rendimiento. Obtenga el rendimiento máximo con señal de f = 1 kHz. -Para representar potencias medias, puede utilizar el comando “Add Trace” en PROBE, y añadir el valor medio de la variable deseada con el operador AVG(). Este operador calcula el valor medio de la variable o variables incluidas en el paréntesis (en este caso un producto de corriente y tensión). El valor medio buscado es el que se obtiene tras integrar en un periodo, por lo que debe leerse el valor en los múltiplos del periodo de la señal (en este caso, 1ms, 2 ms… ). Compare los resultados con lo esperado teóricamente, despreciando los efectos de la distorsión de cruce y la potencia disipada en el operacional.

Para $A_{vd} = 10^6 \ V/V$ obtenemos lo siguiente:

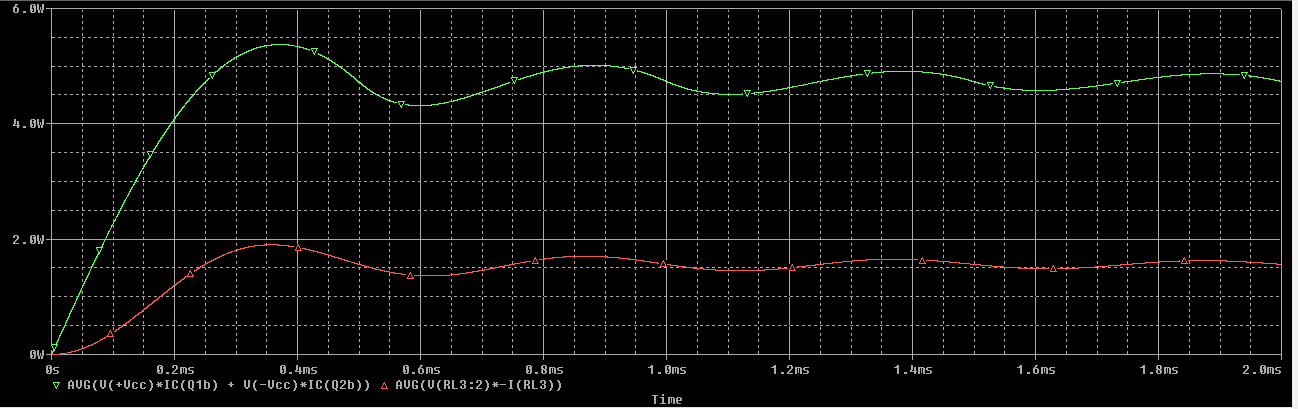
Sabiendo que el rendimiento se obtiene como $\eta = \frac{P_L}{P_{in}}$ se puede calcular dividiendo las dos gráficas de la siguiente forma:

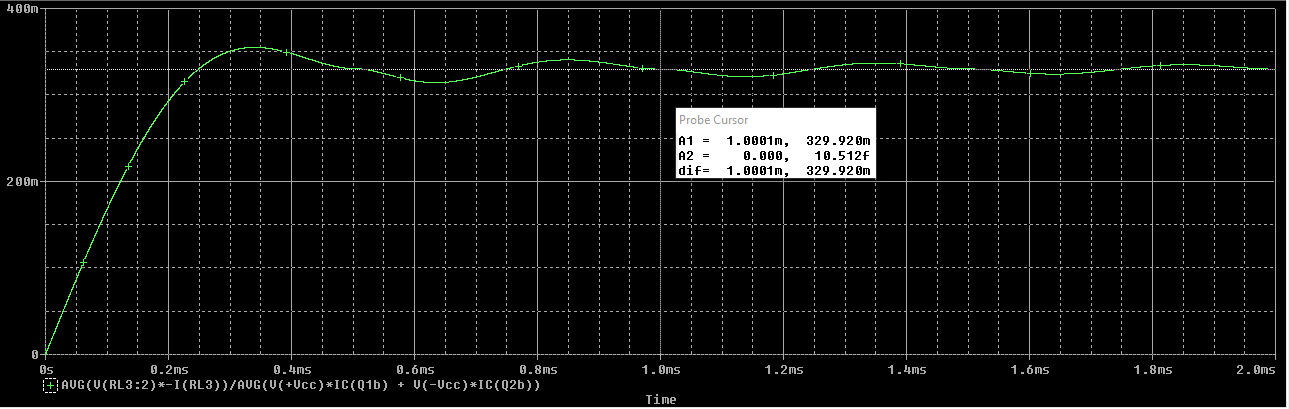
Cuando $t = 1 \ ms$ podemos ver que se cumple lo siguiente: $$\eta = 32.99 \ \%$$

Se ha medido la señal a $t = 1 \ ms$ porque es múltiplo del periodo de la señal.

Ahora probamos para $A_{vd} = 10 \ V/V$

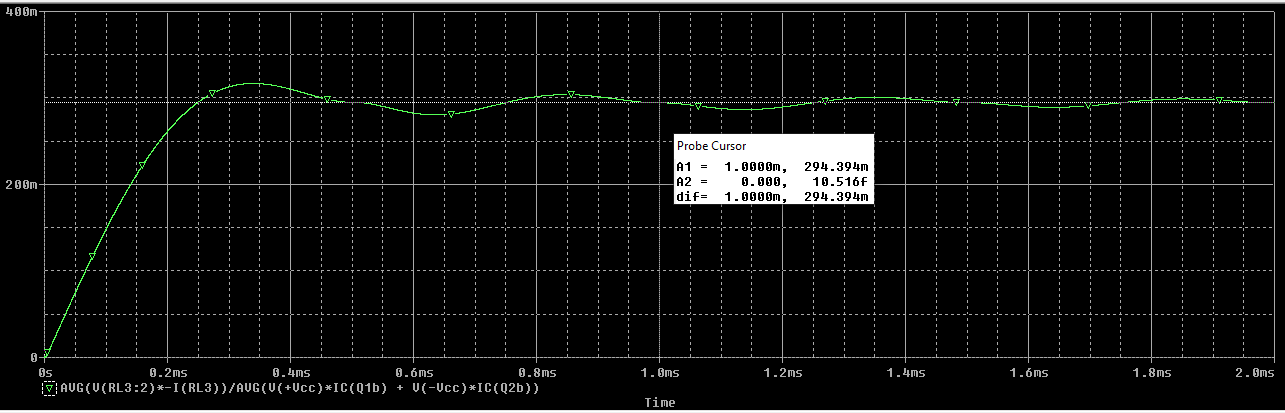
En donde obtenemos que: $$\eta = 29.44 \ \%$$

El valor de rendimiento teórico se obtiene de la siguiente forma: $$\eta = \frac{P_L}{P_{in}}$$

En donde: $$P_L = \frac{1}{2}\frac{V_L^2}{R_L} = \frac{5^2}{2 \cdot 8} = 1.56 \ W \\ $$ La potencia suministrada por la fuente se hallará: $$I_P = \frac{V_L}{R_L} = \frac{5}{8} = 0.625 \ A \\ I_{CC} = \frac{I_P}{\pi} = \frac{0.625}{\pi} = 0.199 \ A \\ P_{in} = 2 \cdot V_{CC} \cdot <I_{CC}> = 2 \cdot 12 \cdot 0.199 = 4.776 \ W$$

Por lo que llegamos a que el rendimiento teórico es: $$\eta = \frac{P_L}{P_{in}} = \frac{1.56}{4.776} = 0.3266 = 32.66 \ \%$$

Que es un valor muy aproximado al obtenido en la simulación con $A_{vd} = 10^6 \ V/V$.

Para $A_{vd} = 10 \ V/V$ se obtendrá la siguiente relación:

$$V_L = V_{i}\frac{A_{vd}}{1 + A_{vd}} - \frac{V_{BE1}}{1 + A_{vd}} \approx V_{i}\frac{A_{vd}}{1 + A_{vd}}$$

Con lo que el rendimiento teórico con $A_{vd} = 10 \ V/V$ será de: $$\eta = \frac{P_L}{P_{in}} = 29.86 \ \%$$

Que es muy próximo al calculado en la simulación con $A_{vd} = 10 \ V/V$.