Métricas de prestaciones
- Tiempo de ejecución / respuesta / latencia $$ T_{CPU} = ciclos \cdot T_{CK} = \frac{ciclos}{f_{CK}} $$
- Velocidad o tasa (throuchput) -> Tareas completadas por unidad de tiempo $$ r = \frac{1}{\text{Tiempo de ejecución}} $$
- Velocidad relativa de X respecto de Y (speedup) $$ S = \frac{\text{Tiempo de ejecución}_Y }{\text{Tiempo de ejecucuón}_X } $$
Prestaciones con un conjunto de programas
- Tiempo de ejecución = media aritmética de tiempos (s) $$ T = \frac{1}{n} \sum_{i} t_i $$
- Velocidad = media armónica de velocidades \(r_i\) (MIPS) $$ r = \frac{ n }{ \sum_{i} (1 / r_i) } $$
- Velocidad relativa \(\approx\) media geométrica de \(S_i\) respecto a R $$ S = \sqrt[n]{\prod_i S_i} $$
Métricas
- Energía dinámica -> Conmutación del transistor de 0 a 1 y viceversa $$ E = \frac{1}{2} \cdot \text{Carga capacitiva} \cdot \text{Voltaje}^2 $$
- Consumo de potencia dinámica -> Se reduce al bajar la frecuencia de reloj $$ P_{\text{dinámica}} = \frac{1}{2} \cdot \text{Carga capacitiva} \cdot \text{Voltaje}^2 \cdot \text{Frecuencia} $$
- Consumo de potencia estática -> Escala con el número de transistores $$ P_{\text{estática}} = \text{Corriente estática} \cdot \text{Voltaje} $$
Con lo que: $$ E = P \cdot T $$
Coste de los circuitos integrados
$$ \text{Coste_IC} = ( \text{Coste_chip} + \text{Coste_encap} + \text{Coste_test}) / \text{Rendimiento} $$ $$ \text{Coste_chip} = \text{Coste_oblea} / \text{Chips por oblea} $$ $$ \text{Chips por oblea} \approx \frac{\text{Area_oblea}}{\text{Area_chip}} $$
Fiabilidad y disponibilidad
- Fiabilidad: Tiempo de cumplimiento del servicio $$ \text{Fiabilidad} = \text{MTFF} $$
- Disponibilidad: Fracción del tiempo que el servicio cumple de acuerdo con las especificaciones. Siendo MTTR el tiempo medio de reparación $$ \text{Disponibilidad} = \frac{\text{MTTF}}{\text{MTBF}} \qquad \lvert \text{MTBF} = \text{MTTF} + \text{MTTR} $$
Ley de Amdahl (I)
Cuantifica el impacto en las prestaciones de una mejora según lo habitual que sea -> meejorar lo frecuente $$ T = T_{ant} \cdot [(1 - F_m) + F_m / S_m] $$
- \(T\) : Tiempo de ejecución tras una mejora
- \(T_{ant}\) : Tiempo de ejecución antes de la mejora
- \(F_m\) : Fracción del tiempo en la que se aplica la mejora
- \(S_m\) : Incremento de velocidad durante la mejora
$$ S = \frac{T_{ant}}{T} = \frac{1}{(1-F_m) + \frac{F_m}{S_m}} $$
- \(S\): Incremento de velocidad global (speedup)
- Máxima mejoría global posible: \(S_{max} = \frac{1}{(1 - F_m)}\)
Ecuación del tiempo de CPU
$$ T_{CPU} = \text{IC} \cdot \text{CPI} \cdot T_{CK} \Rightarrow T_{CPU} = (\sum_{i} IC_i \cdot \text{CPI}i) \cdot T{CK} $$
- IC: Número de instrucciones del programa (instruction count)
- CPI: Ciclos de reloj por instrucción
Alguna cosilla importante
$$ \text{MIPS (Millones de instrucciones por seg)} = \frac{IC}{10^6}\cdot \frac{1}{T_{CPU}} = \frac{f_{CK}}{\text{CPI} \cdot 10^6} $$
Ejecicio típico de cambio de CPU y tal
Cuando una parte del programa se puede paralelizar con 4 cores.
$$ S = \frac{T_{ant}}{T_{act}}= \frac{ \text{ciclos-ant} \cdot 1/f_{ant}}{\text{ciclos-act} \cdot 1/f_{act}} = \frac{1/f_{ant}}{[(F_p / 4)+ (1 - F_p)] \cdot 1/f_{act}} $$
Ejercicio típico de ahorro de bateria
Nos dice que el procesador actual usa el 40%, se cambia po otro que que reduce un 10% la frecuencia y la tension de alimentación. ¿Qué porcentaje se alargará la vida?
$$ 0.4 \cdot E1 = \frac{1}{2} \cdot C \cdot V^2 \\ E2 = E1 * (1-0.4) + \frac{1}{2}\cdot C \cdot (0.9 \cdot V)^2 \\ \text{Resultado} = E1 / E2 $$
Ejercicio típico de la características del procesador con emisión múltiple

$$ \text{Ciclos por predicción incorrecta} = (\text{etapa en la que se ejecutan los saltos} - 1) + \\ \frac{\sum_{i = 0}^{\text{instr emitidas por ciclo - 1}} i / \text{instr emitidas por ciclo}}{\text{Intruscciones emitidas por ciclo}} \\ = (7-1)+(0/4 + 1/4 + 2/4 + 3/4)/4 = 6,375 $$
$$ CPI_{\text{ideal}} = 1 / \text{instrucciones emitidas por ciclo} = 1/4 $$
Ejercicio típico - Cambiar porcentajes de aparición de alguna instruccion
$$ T_{instr} = \frac{CPI_{instr} \cdot F_i}{CPI_{prom} \cdot (1 - F_i) + CPI_{instr} \cdot F_i} $$
Ejercicio típico - Ahorro de potencia cambiando porcentajes de aparicion de alguna instruccion
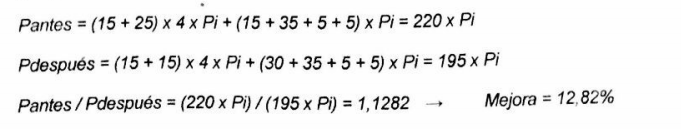
Ejercicio típico - Ahorro de energía cuando cambio de compilador
